数据结构与算法
1.链表
1.1单向链表
1.1.1单向链表概述
单链表是一种链式存取的数据结构,用一组地址任意的存储单元存放线性表中的数据元素。链表中的数据是以结点来表示的,每个结点的构成:元素+ 指针(指示后继元素存储位置),元素就是存储数据的存储单元,指针就是连接每个结点的地址数据。
链表有两个比较重要的部分组成:
- 指针指向下一个节点的地址,(即内存位置的直接地址)
- 节点链表中的组成部分,对于单链表,一个节点里面包含节点数据和下一个节点的指针
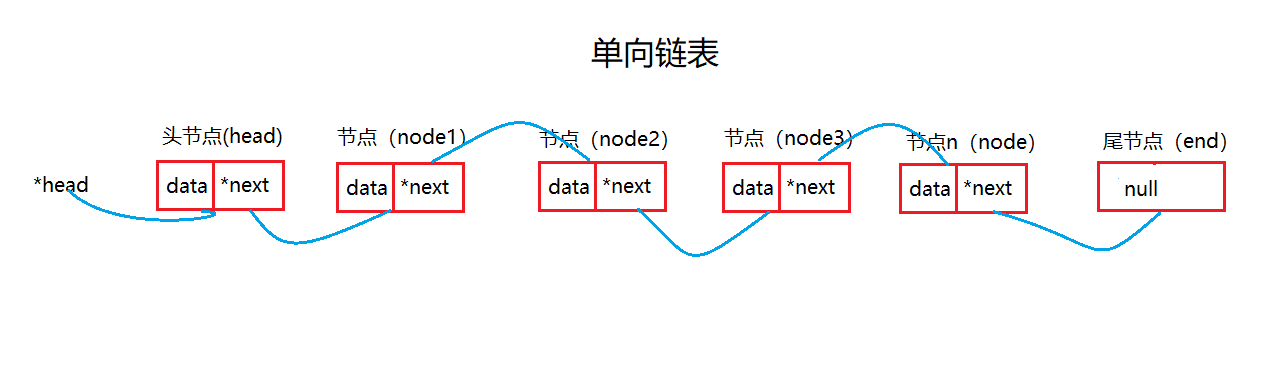
- 链表是以节点的方式来存储,是链式存储
- 每个节点包含data域和指针域
- 如图:链表的各个节点不一定是连续存储,只是逻辑结构上连续,物理结构上不一定连续
- 链表分带头节点的链表和没有头节点的链表,根据实际的需求来确定
带头结点的单向链表示意图如下:
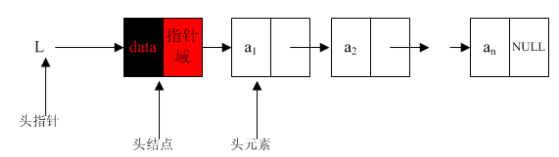
没有头节点,则头指针直接指向头节点
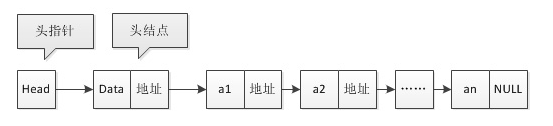
1.1.2单向链表的实现
1.1.2.1添加节点——默认添加到链表尾部
使用带头结点的单向链表,实现水浒英雄排行榜对英雄人物的增删改查操作。
- 先创建一个head头节点,作用就是表示单链表的头节点
- 首先查找到next域为null的节点,该节点就是尾节点
- 每添加一个节点,就直接加入到链表的最后
- 通过一个辅助遍历整个链表
创建HeroNode对象,每一个对象就是一个节点
- HeroNode类
- 节点类,包含data域和next域
public class HeroNode {
//data域
int no;
String name;
//next域
HeroNode next; //指向下一个节点
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
@Override
public String toString() {
return "HeroNode{" +
"no=" + no +
", name='" + name + '\'' +
'}';
}
}- SingleLinked类
public class SingleLinked {
/**
* 初始化头节点
*/
private HeroNode head = new HeroNode(0, "");
/**
* 添加节点到单向链表
* 思路:1.找到当前链表的最后节点
* 2.将最后节点的next指向新的节点
*
* @param heroNode 英雄节点
*/
public void add(HeroNode heroNode) {
// 1.因为head头节点不可变,创建中间节点变量指向head
HeroNode temp = head;
while (true) {
// 2.如果此时为尾节点,结束循环
if (temp.next == null) {
break;
}
// 3.不是尾节点就指向下一节点
temp = temp.next;
}
// 4.在末尾添加新节点
temp.next = heroNode;
}
/**
* 按照顺序添加节点
*
* @param heroNode 英雄节点
*/
public void addByOrder(HeroNode heroNode) {
// 1.因为head头节点不可变,创建中间节点变量指向head
HeroNode temp = head;
// 2.flag用于判断是否存在Node
boolean flag = false;
while (true) {
// 3.如果此时为尾节点,结束循环
if (temp.next == null) {
break;
}
// 4.找出要插入的位置
if (temp.next.no > heroNode.no) {
break;
} else if (temp.next.no == heroNode.no) { //存在相等元素
flag = true;
break;
}
// 5.指向下一节点
temp = temp.next;
}
if (flag) {
System.out.println("已经存在对应编号的Node");
} else {
heroNode.next = temp.next;
temp.next = heroNode;
}
}
}- 测试类
public class TestDemo {
public static void main(String[] args) {
SingleLinked singleLinked = new SingleLinked();
HeroNode heroNode1 = new HeroNode(1, "宋江");
HeroNode heroNode2 = new HeroNode(2, "卢俊义");
HeroNode heroNode3 = new HeroNode(3, "吴用");
HeroNode heroNode4 = new HeroNode(4, "林冲");
singleLinked.add(heroNode1);
singleLinked.add(heroNode2);
singleLinked.add(heroNode3);
singleLinked.add(heroNode4);
singleLinked.list();
}
}
1.1.2.2添加节点——优化添加到指定位置
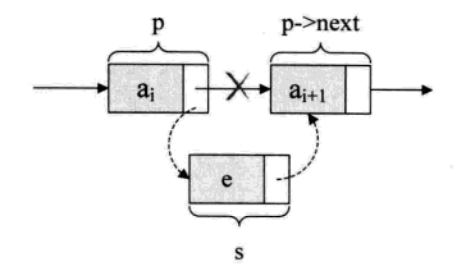
- 首先判断新节点要添加的位置,找到
next域为null的节点,该节点就是尾节点。- 对于添加节点的前一个节点为temp,则
newNode.next = temp.next,temp.next = newNode
- SingleLinked类
- 添加
addByOrder方法
- 添加
/**
* 按照顺序添加节点
*
* @param heroNode 英雄节点
*/
public void addByOrder(HeroNode heroNode) {
// 1.因为head头节点不可变,创建中间节点变量指向head
HeroNode temp = head;
// 2.flag用于判断是否存在Node
boolean flag = false;
while (true) {
// 3.如果此时为尾节点,结束循环
if (temp.next == null) {
break;
}
// 4.找出要插入的位置
if (temp.next.no > heroNode.no) {
break;
} else if (temp.next.no == heroNode.no) { //存在相等元素
flag = true;
break;
}
// 5.指向下一节点
temp = temp.next;
}
if (flag) {
System.out.println("已经存在对应编号的Node");
} else {
heroNode.next = temp.next;
temp.next = heroNode;
}
}
/**
* 遍历链表
*/
public void list() {
if (head.next == null) {
return;
}
HeroNode temp = head.next;
while (true) {
// 1.到达链表尾部,结束循环
if (temp == null) {
break;
}
System.out.println(temp);
// 2.temp后移到下一个节点
temp = temp.next;
}
}- 测试类
- 按照no添加
public class TestDemo {
public static void main(String[] args) {
SingleLinked singleLinked = new SingleLinked();
HeroNode heroNode1 = new HeroNode(1, "宋江");
HeroNode heroNode2 = new HeroNode(2, "卢俊义");
HeroNode heroNode3 = new HeroNode(3, "吴用");
HeroNode heroNode4 = new HeroNode(4, "林冲");
singleLinked.addByOrder(heroNode1);
singleLinked.addByOrder(heroNode3);
singleLinked.addByOrder(heroNode4);
singleLinked.addByOrder(heroNode2);
singleLinked.list();
}
}
1.2.2.3修改节点
- 查找到对应的节点,修改信息
- SingleLinked类
- 添加update方法
/**
* 修改节点信息,只能根据no修改name信息
*
* @param heroNode 英雄节点
*/
public void update(HeroNode heroNode) {
HeroNode temp = head.next;
// 1.判断是否找到该节点
boolean flag = false;
while (true) {
// 2.如果达到链表末尾,结束循环
if (temp == null) {
break;
}
// 3.查找到了要修改的节点,结束
if (temp.no == heroNode.no) {
flag = true;
break;
}
temp = temp.next;
}
if (flag) {
temp.name = heroNode.name;
} else {
System.out.println("该节点不存在!");
}
}- 测试类
public class TestDemo {
public static void main(String[] args) {
SingleLinked singleLinked = new SingleLinked();
HeroNode heroNode1 = new HeroNode(1, "宋江");
HeroNode heroNode2 = new HeroNode(2, "卢俊义");
HeroNode heroNode3 = new HeroNode(3, "吴用");
HeroNode heroNode4 = new HeroNode(4, "林冲");
singleLinked.addByOrder(heroNode1);
singleLinked.addByOrder(heroNode3);
singleLinked.addByOrder(heroNode4);
singleLinked.addByOrder(heroNode2);
singleLinked.update(new HeroNode(1,"姚盖"));
singleLinked.list();
}
}
1.2.3.4删除节点
- 查找到要删除的节点,将删除节点的前一个节点指向删除节点的后一个节点
- 将删除节点的前一个节点,并指向删除节点的后一个节点,被删除的节点在内存中不存在引用,后续被GC回收。
/**
* 删除节点,将删除节点的前一个节点指向删除节点的后一个节点
*
* @param no 要删除的节点编号
*/
public void delete(int no) {
HeroNode temp = head;
boolean flag = false;
while (true) {
if (temp.next == null) {
System.out.println("未找到要删除的节点!");
break;
}
// 2.找到要删除的节点的前一个节点
if (temp.next.no == no) {
flag = true;
break;
}
// 3.指向下一节点
temp = temp.next;
}
if (flag) {
// 4.删除的节点的前一个节点就指向删除节点下一节点的节点
temp.next = temp.next.next;
} else {
System.out.println("未找到要删除的节点!");
}
}- 测试类
public class TestDemo {
public static void main(String[] args) {
SingleLinked singleLinked = new SingleLinked();
HeroNode heroNode1 = new HeroNode(1, "宋江");
HeroNode heroNode2 = new HeroNode(2, "卢俊义");
HeroNode heroNode3 = new HeroNode(3, "吴用");
HeroNode heroNode4 = new HeroNode(4, "林冲");
singleLinked.addByOrder(heroNode1);
singleLinked.addByOrder(heroNode3);
singleLinked.addByOrder(heroNode4);
singleLinked.addByOrder(heroNode2);
singleLinked.delete(1);
singleLinked.list();
}
}
1.1.3单向链表案例
1.1.3.2获取到单向链表的节点个数
要求:如果是带头节点的链表,不统计头节点
/**
* 得到除头节点外的节点数量
*/
/**
* 得到除头节点外的节点数量
*/
public void getNumber() {
int number = 0;
HeroNode temp = head.next;
while (temp != null){
number++;
temp = temp.next;
}
return number;
}1.1.3.1链表中倒数第k个节点
输入一个链表,输出该链表中倒数第k个节点。为了符合大多数人的习惯,本题从1开始计数,即链表的尾节点是倒数第1个节点。
例如,一个链表有 6 个节点,从头节点开始,它们的值依次是 1、2、3、4、5、6。这个链表的倒数第 3 个节点是值为 4 的节点。
示例:
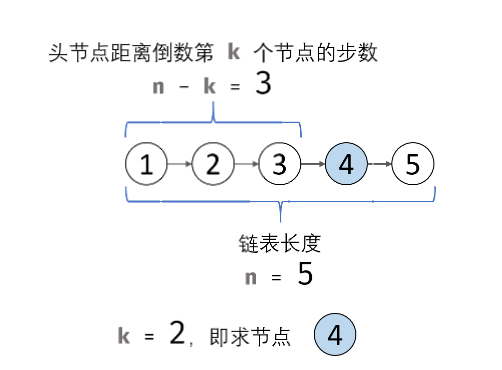
给定一个链表: 1->2->3->4->5, 和 k = 2.
返回链表 4->5.思路:求出链表中的倒数第K个节点,即指针从头节点向后移动
链表长度 - K个节点。
class Solution {
public ListNode getKthFromEnd(ListNode head, int k) {
// 1.首先遍历此单向链表,得出除头节点外的所有节点长度
int number = 0;
ListNode temp = head;
while (temp != null) {
number++;
temp = temp.next;
}
// 2.如果要查找倒数第几个节点,那么就用链表的长度减去倒数的第几个节点
temp = head;
while (number - k > 0) {
temp = temp.next;
number--;
}
return temp;
}
}1.2双向链表
1.2.1单向链表的缺点
- 单向链表,查找的方向只能是一个方向,而双向链表可以向前或者向后查找。
- 单向链表不能自我删除,需要靠辅助节点,而双向链表,则可以自我删除,所以前面我们单向链表删除时节点,总是找到temp,temp是待删除节点的前一个节点。
1.2.2双向链表概述
双向链表又叫做双链表;跟单向链表不同的是,他的每个节点都有两个指针,一个指向前面的一个节点,一个指向后面的节点。通过这两个指针我们可以很方便的通过某一个节点,访问到相(前)邻(后)的两个节点。
- 同单链表类似由一个一个的节点组成
- 与单向链表不同的是,每个节点中包含了除数据(
data)之外的上一个节点的指针(*prev)和下一个节点的指针(*next)
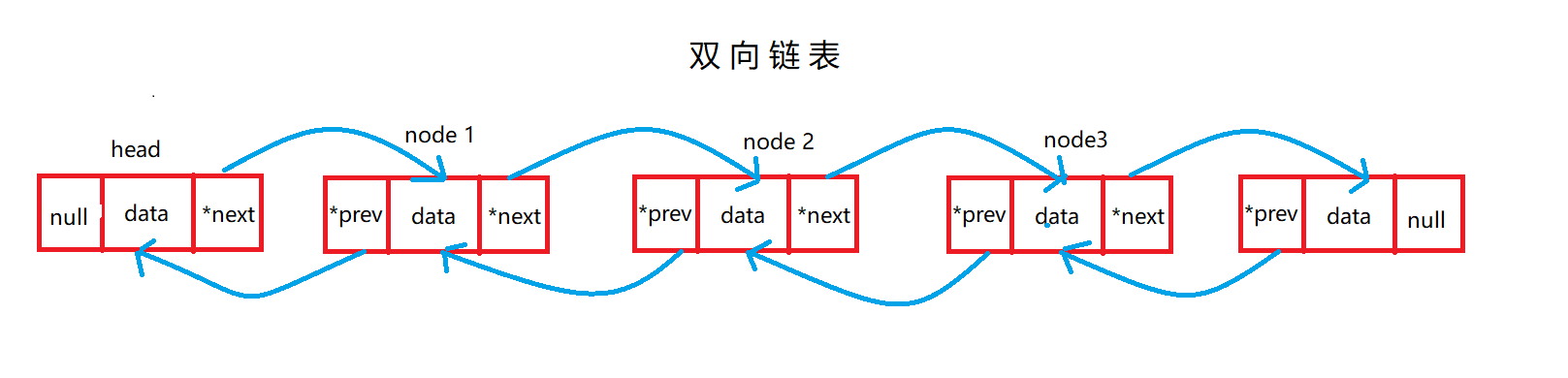
图中我们可以看到,除了头节点和尾节点之外,每个中间节点与节点之间都是首尾相连,每个节点保存了上一个节点的指针和下一个节点的指针,这就是与单链表的不同之处。
注:我们也可以构造双向循环链表;尾节点的下一个指针*next指向头节点,而头节点的*prev指向尾节点;这样就构成了一个双向循环链表;下图所示,我们只需把双向链表简单改造一下即可:
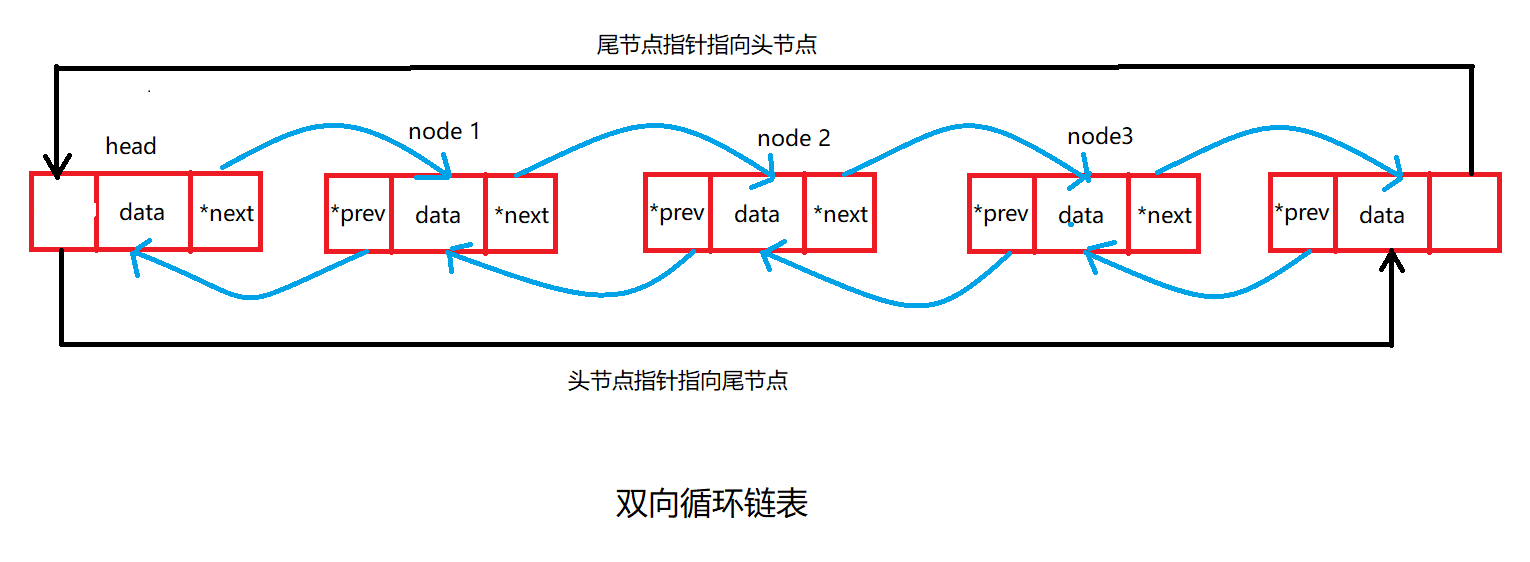
1.2.3分析双向链表的遍历,添加,修改,删除的操作思路:
遍历
- 遍历和单向链表类似,只是可以向前,也可以向后查找。
添加(默认添加到双向链表的最后):
- 先找到双向链表的最后这个节点
temp.next=newHeroNode;
newHeroNode.pre=temp;
修改
- 修改和的单向链表相同。
删除:
因为是双向链表,因此,我们可以实现自我删除某个节点
直接找到要删除的这个节点,比如temp
temp.pre.next=temp.next;
temp.next.pre=temp.pre;
1.2.4双向链表实现
1.2.4.1添加节点——默认添加到链表尾部
- HeroNode节点类,添加
前驱节点和后继节点
public class HeroNode {
//data域
int no;
String name;
//pre
HeroNode pre; //指向上一个节点
//next
HeroNode next; //指向下一个节点
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
@Override
public String toString() {
return "HeroNode{" +
"no=" + no +
", name='" + name + '\'' +
'}';
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
}- DoubleLinked类定义添加方法add()
- 只需要将添加的节点,添加到链表末尾。即将尾节点的next指针指向新节点,将新节点的pre指针指向尾节点。
public class DoubleLinked {
// 1.创建头节点
private final HeroNode head = new HeroNode(0, "");
/**
* 添加节点,添加到双向链表尾部
*
* @param heroNode 英雄节点
*/
public void add(HeroNode heroNode) {
HeroNode temp = head;
while (true) {
// 1.找到尾节点
if (temp.next == null) {
break;
}
temp = temp.next;
}
// 2.添加新节点
temp.next = heroNode;
heroNode.pre = temp;
}
/**
* 遍历链表
*/
public void list(){
HeroNode temp = head.next;
while (true){
if (temp == null){
break;
}
System.out.println(temp);
temp = temp.next;
}
}
}
测试类:
public class TestDemo {
public static void main(String[] args) {
DoubleLinked doubleLinked = new DoubleLinked();
HeroNode heroNode1 = new HeroNode(1, "宋江");
HeroNode heroNode2 = new HeroNode(2, "卢俊义");
HeroNode heroNode3 = new HeroNode(3, "吴用");
HeroNode heroNode4 = new HeroNode(4, "林冲");
doubleLinked.add(heroNode1);
doubleLinked.add(heroNode2);
doubleLinked.add(heroNode3);
doubleLinked.add(heroNode4);
doubleLinked.list();
}
}
1.1.2.2添加节点——优化添加到指定位置
在循环中,需要比较
temp.next节点的属性值与新节点的属性值。如果temp.next节点的属性值大于新节点的属性值,则跳出循环。否则,将temp指向下一个节点并继续循环。当找到插入位置后,在添加新节点时,应该先检查
temp.next是否为null,然后再执行temp.next.pre = heroNode;。当在双向链表的末尾添加一个新节点时,
temp.next将为null。在这种情况下,我们不需要设置新节点的前驱节点,因为新节点已经是链表的最后一个节点了。因此,我们需要先检查temp.next是否为null,然后再执行temp.next.pre = heroNode;。
/**
* 按顺序添加节点
*
* @param heroNode 英雄节点
*/
public void addByOrder(HeroNode heroNode) {
HeroNode temp = head;
boolean flag = false;
while (true) {
// 1.查找到尾节点
if (temp.next == null) {
break;
}
// 2.判断节点顺序
if (temp.next.no > heroNode.no) {
break;
} else if (temp.next.no == heroNode.no) {
flag = true;
break;
}
temp = temp.next;
}
if (flag) {
System.out.println("已存在当前节点!");
} else {
// 3.添加新节点
// 3.1新添加的节点的后继节点为添加前一个节点的下一个节点
heroNode.next = temp.next;
if (temp.next != null) {
temp.next.pre = heroNode;
}
// 3.2添加前一个节点的后继节点指向新节点
temp.next = heroNode;
// 3.3新节点的前驱节点为添加的前一个节点
heroNode.pre = temp;
}
}测试类:
public class TestDemo {
public static void main(String[] args) {
DoubleLinked doubleLinked = new DoubleLinked();
HeroNode heroNode1 = new HeroNode(1, "宋江");
HeroNode heroNode2 = new HeroNode(2, "卢俊义");
HeroNode heroNode3 = new HeroNode(3, "吴用");
HeroNode heroNode4 = new HeroNode(4, "林冲");
doubleLinked.addByOrder(heroNode1);
doubleLinked.addByOrder(heroNode4);
doubleLinked.addByOrder(heroNode2);
doubleLinked.addByOrder(heroNode3);
doubleLinked.list();
}
}
1.2.4.2修改节点
- 查找到对应的节点,修改信息
SingleLinked类
- 添加update方法
/**
* 修改节点
*
* @param heroNode 英雄节点
*/
public void update(HeroNode heroNode){
HeroNode temp = head.next;
boolean flag = false;
while (true){
if (temp == null){
break;
}
if (heroNode.no == temp.no){
flag = true;
temp.name = heroNode.name;
}
temp = temp.next;
}
if (!flag){
System.out.println("修改的节点不存在!");
}
}测试类:
public class TestDemo {
public static void main(String[] args) {
DoubleLinked doubleLinked = new DoubleLinked();
HeroNode heroNode1 = new HeroNode(1, "宋江");
HeroNode heroNode2 = new HeroNode(2, "卢俊义");
HeroNode heroNode3 = new HeroNode(3, "吴用");
HeroNode heroNode4 = new HeroNode(4, "林冲");
doubleLinked.add(heroNode1);
doubleLinked.add(heroNode2);
doubleLinked.add(heroNode3);
doubleLinked.add(heroNode4);
doubleLinked.delete(new HeroNode(1,"姚盖"));
doubleLinked.list();
}
}
1.2.4.3删除节点
- 删除节点就是将删除节点的前一个结点的next指针指向删除节点的下一个节点
- 将删除节点的下一个节点的pre指针指向删除节点的前一个节点
/**
* 删除节点
*
* @param heroNode 英雄节点
*/
public void delete(HeroNode heroNode) {
boolean flag = false;
if (head.next == null) {
System.out.println("链表为空!");
}
HeroNode temp = head.next;
while (true) {
if (temp == null) {
break;
}
if (heroNode.no == temp.no) {
flag = true;
// 1.将删除节点的前一个节点的next指向删除节点的后一个节点
temp.pre.next = temp.next;
// 2.必须不是最后一个节点,否则会出现空指针异常,因为最后一个节点的next为null
if (temp.next != null) {
// 3.将删除节点的后一个节点的pre指向删除节点的前一个节点
temp.next.pre = temp.next;
}
break;
}
temp = temp.next;
}
if (!flag) {
System.out.println("修改的节点不存在!");
}
}测试类:
public class TestDemo {
public static void main(String[] args) {
DoubleLinked doubleLinked = new DoubleLinked();
HeroNode heroNode1 = new HeroNode(1, "宋江");
HeroNode heroNode2 = new HeroNode(2, "卢俊义");
HeroNode heroNode3 = new HeroNode(3, "吴用");
HeroNode heroNode4 = new HeroNode(4, "林冲");
doubleLinked.add(heroNode1);
doubleLinked.add(heroNode2);
doubleLinked.add(heroNode3);
doubleLinked.add(heroNode4);
doubleLinked.delete(new HeroNode(1,"宋江"));
doubleLinked.list();
}
}
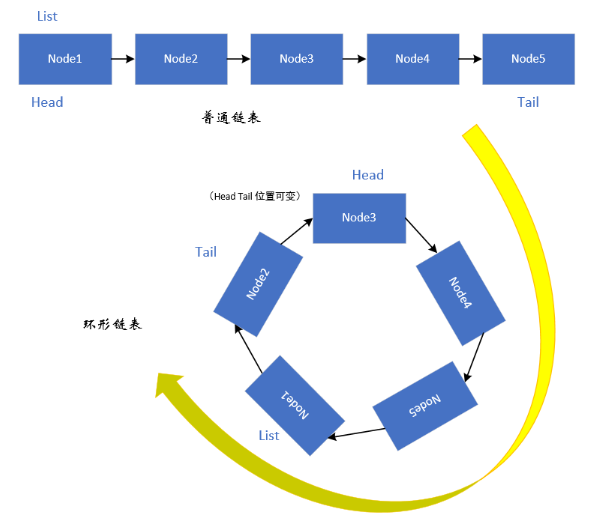
1.3单向环形链表
1.3.1单向环形链表概述
单向环形链表是一种特殊的链表,它的最后一个节点指向第一个节点,形成一个环。与普通的单向链表不同,单向环形链表没有任何节点的next指针为null。
单向环形链表可以用来解决一些特定的问题,例如约瑟夫问题。
1.3.2单向环形链表的实现
- CyclingLinked类,创建环形结构
定义一个变量
currentNode来表示当前节点。接下来,使用一个循环来添加节点。在每次循环中,创建一个新的节点,并根据当前循环的次数设置节点的编号。如果这是第一个节点,则将其设置为链表的第一个节点,并将其
next指针指向自己,以形成一个环。否则,将当前节点的next指针指向新节点,并将新节点的next指针指向第一个节点,以保持环形结构。最后,将当前节点更新为新节点。
public class CyclingLinked {
// 1.表示首节点
public static Node firstNode = null;
public static void add(int nums) {
if (nums < 1) {
System.out.println("节点个数不正确");
return;
}
// 2.表示当前节点
Node currentNode = null;
for (int i = 1; i <= nums; i++) {
Node node = new Node(i);
// 如果只有一个节点,将该节点指向自己形成环形结构
if (i == 1) {
firstNode = node;
firstNode.next = firstNode;
currentNode = firstNode;
}
// 尾节点的后继节点就是新节点
currentNode.next = node;
// 新节点的后继节点指向头节点形成环形结构
node.next = firstNode;
// 当前节点就是新节点
currentNode = node;
}
}
}- 遍历循环链表
/**
* 输出循环链表
*/
public static void list() {
Node currentNode = firstNode;
while (true) {
System.out.println(currentNode);
if (currentNode.next == firstNode) {
break;
}
currentNode = currentNode.next;
}
}
1.3.3约瑟夫环(Josephu)问题
1.3.3.1问题介绍
约瑟夫问题(约瑟夫环、丢手绢问题)为:设编号为1,2,…n的n个人围坐一圈,约定编号为k(1<=k<=n)的人从1开始报数,数到m的那个人出列,它的下一位又从1开始报数,数到m的那个人又出列,依次类推,直到所有人出列为止,由此产生一个出队编号的序列。
1.3.3.2解决方法即思路
解决方法:用一个不带头结点的循环链表来处理Josephu问题:先构成一个有n个结点的单循环链表,然后由k结点起从1开始计数,计到m时,对应结点从链表中删除,然后再从被删除结点的下一个结点又从1开始计数,直到最后一个结点从链表中删除算法结束。
- JosepfuCycling类
辅助指针
helper指向链表的最后一个节点是为了方便删除节点。在约瑟夫环问题中,每次都要删除第m个节点,而在单向链表中,要删除一个节点,我们需要知道它的前一个节点。因此,我们使用辅助指针helper来跟踪当前节点的前一个节点。在模拟游戏过程时,我们从当前节点开始遍历链表,每次都让
firstNode和helper同时向后移动一位,直到找到第m个节点。此时,firstNode指向的就是要删除的节点,而helper指向的就是要删除节点的前一个节点。我们可以通过修改helper.next的值来删除firstNode指向的节点。
public class JosepfuCycling {
public int josepfu(int nums, int space) {
// 1.首先创建单向循环链表
CyclingLinked.add(nums);
// 2.获取首节点
Node firstNode = CyclingLinked.firstNode;
// 3.创建辅助节点
Node helper = firstNode;
// 4.将helper指向firstNode的前一个节点
while (helper.next != firstNode) {
helper = helper.next;
}
while (nums > 0) {
// 3.firstNode和helper同时移动space-1次
for (int i = 0; i < space - 1; i++) {
firstNode = firstNode.next;
helper = helper.next;
}
// 4.此时firstNode指向的节点就是要出圈的节点,更改firstNode和helper的指向,
// firstNode指向下一个节点,helper指向firstNode
firstNode = firstNode.next;
helper.next = firstNode;
nums--;
}
return firstNode.no;
}
}- 测试类:
public class TestDemo {
public static void main(String[] args) {
JosepfuCycling josepfuCycling = new JosepfuCycling();
int result = josepfuCycling.josepfu(5, 2);
System.out.println(result);
}
}
2.栈
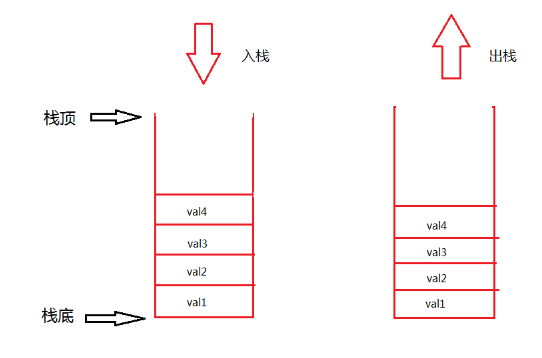
2.1栈的概念
栈(stack)又名堆栈,它是一种运算受限的线性表。其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶,相对地,把另一端称为栈底。向一个栈插入新元素又称作入栈(push),它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素;从一个栈删除元素又称作出栈(pop),它是把栈顶元素删除掉,使其相邻的下一个元素成为新的栈顶元素。
2.2栈的应用场景
- 子程序的调用:在跳往子程序前,会先将下个指令的地址存到堆栈中,直到子程序执行完后再将地址取出, 回到原来的程序中。
- 处理递归调用:和子程序的调用类似,只是除了储存下一个指令的地址外,也将参数、区域变量等数据存入堆栈中。
- 表达式的转换[中缀表达式转后缀表达式]与求值(实际解决)。
- 二叉树的遍历。
- 图形的深度优先(depth一first)搜索法。
2.3数组实现栈
使用数组来模拟栈的思路:
- 初始化栈:创建一个stack数组,指定数组长度,创建一个top标记,初始值为-1。
- 元素入栈:当向数组中添加元素的时候,top++,表示的索引下标为栈顶。
- 元素出栈:取出stack数组中的位于top的元素。
- 打印栈:倒叙遍历数组。
- ArrayStack类
- 实现了初始化栈、判断栈是否为空、判断栈是否满、元素入栈、元素出栈、得到栈顶元素、遍历链表
public class ArrayStack {
private int maxSize;
private int[] stack;
private int top = -1;
// 有参构造,初始化栈
public ArrayStack(int maxSize) {
this.maxSize = maxSize;
stack = new int[maxSize];
}
/**
* 判断栈是否为空
* 当top = -1的时候,栈就为空
*
* @return boolean
*/
public boolean isEmpty() {
return top == -1;
}
/**
* 判断栈是否满
* 当top = maxSize时,栈就为满
*
* @return boolean
*/
public boolean isFull() {
return top == maxSize;
}
/**
* 入栈操作
*
* @param value 价值
*/
public void push(int value) {
// 1.首先判断栈是否满了
if (isFull()) {
throw new RuntimeException("栈已经满了");
}
// 2.将元素压入栈中
top++;
stack[top] = value;
}
/**
* 出栈操作
*/
public int pop() {
// 1.首先判读栈是否为空
if (isEmpty()) {
System.out.println("栈为空");
return -1;
}
int result = stack[top];
top--;
return result;
}
/**
* 得到栈顶元素
*
* @return int
*/
public int getTop(){
return stack[top];
}
/**
* 遍历栈
*/
public void list(){
// 1.判断是否栈空
if (isEmpty()){
System.out.println("栈为空");
return;
}
for (int i = top; i >= 0 ; i--) {
System.out.println(stack[i]);
}
}
}- 测试类
public class ArrayStackDemo {
public static void main(String[] args) {
ArrayStack arrayStack = new ArrayStack(5);
arrayStack.push(1);
arrayStack.push(2);
arrayStack.push(3);
arrayStack.push(4);
arrayStack.push(5);
arrayStack.list();
System.out.println("------>栈顶元素出栈");
arrayStack.pop();
arrayStack.list();
}
}
2.4前缀表达式(波兰式)
2.4.1介绍
前缀表达式又称波兰式,前缀表达式的运算符位于操作数之前。举例说明: (3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6
2.4.2前缀表达式的计算机求值
从右至左扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(栈顶元素 和 次顶元素),并将结果入栈;重复上述过程直到表达式最左端,最后运算得出的值即为表达式的结果。
例如: (3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6 , 针对前缀表达式求值步骤如下:
- 从右至左扫描,将6、5、4、3压入堆栈
- 遇到+运算符,因此弹出3和4(3为栈顶元素,4为次顶元素),计算出3+4的值,得7,再将7入栈
- 接下来是×运算符,因此弹出7和5,计算出7×5=35,将35入栈
- 最后是-运算符,计算出35-6(栈顶元素 - 次顶元素)的值,即29,由此得出最终结果
2.5中缀表达式
2.5.1介绍
中缀表达式就是常见的运算表达式,如(3+4)×5-6
2.5.2中缀表达式的计算机求值
使用栈完成中缀表达式的计算思路:
需要创建两个栈:数栈存放数字,符号栈存放运算符
通过一个 index 值(索引),来遍历我们的表达式
如果我们发现是一个数字, 就直接入数栈
如果发现扫描到是一个运算符, 就分如下情况:
如果当前的符号栈为空,就直接入栈。
如果符号栈有运算符,就进行比较:①当前运算符的优先级 <=** 栈中的操作符, 就需要从数栈中pop出两个数,再从符号栈中pop出一个运算符,进行运算,将得到结果压入数栈,然后将当前运算符压入符号栈。②当前运算符的优先级 **> 栈中的操作符, 就直接入符号栈。
当表达式扫描完毕,就顺序的从数栈和符号栈中pop出相应的数和符号,并运行
最后在数栈只有一个数字,就是表达式的结果
2.6后缀表达式(逆波兰表达式)
2.6.1介绍
后缀表达式又称逆波兰表达式,与前缀表达式相似,只是运算符位于操作数之后
举例说明: (3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 –
| 正常表达式 | 逆波兰表达式 |
|---|---|
| a+b | a b + |
| a+(b-c) | a b c - + |
| a+(b-c)*d | a b c - d * + |
| a+d*(b-c) | a d b c - * + |
| a=1+3 | a 1 3 + = |
2.6.2后缀表达式的计算机求值
从左至右扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(次顶元素 和 栈顶元素),并将结果入栈;重复上述过程直到表达式最右端,最后运算得出的值即为表达式的结果。
例如: (3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 - , 针对后缀表达式求值步骤如下:
- 从左至右扫描,将3和4压入堆栈;
- 遇到+运算符,因此弹出4和3(4为栈顶元素,3为次顶元素),计算出3+4的值,得7,再将7入栈;
- 将5入栈;
- 接下来是×运算符,因此弹出5和7,计算出7×5=35,将35入栈;
- 将6入栈;
- 最后是-运算符,计算出35-6的值(次顶元素 - 栈顶元素),即29,由此得出最终结果
2.7逆波兰计算器的实现
- 输入逆波兰表达式,从左到右遍历
- 如果当前符号为数字,则直接入栈。
- 如果当前符号为运算符,则取出栈顶元素和次顶元素,根据元素符进行运算,并将运算结果入栈。直到逆波兰表达式最右侧则结束。
import java.util.Arrays;
import java.util.List;
import java.util.Stack;
public class PolandNotation {
/**
* 将字符串转化为字符集合
*
* @param suffixExpression 后缀表达式
* @return {@link List}<{@link String}>
*/
public static List<String> getListString(String suffixExpression) {
// 1.将字符串通过空格分割成字符串数组
String[] split = suffixExpression.split(" ");
List<String> list = Arrays.asList(split);
return list;
}
/**
* 计算
*
* @param list 列表
* @return int
*/
public static int calculate(List<String> list) {
// 1.创建栈
Stack<String> stack = new Stack<>();
for (String string : list) {
// 2.如果取到的符号是一个多位数,则直接入栈
if (string.matches("^\\d{1,}$")) {
stack.push(string);
} else {
int num1 = 0;
int num2 = 0;
int num3 = 0;
// 3.如果是运算符,则去除栈顶元素和次顶元素
num1 = Integer.parseInt(stack.pop());
num2 = Integer.parseInt(stack.pop());
// 3.1判断运算符
if (("+").equals(string)) {
num3 = num1 + num2;
} else if (("-").equals(string)) {
num3 = num2 - num1;
} else if (("*").equals(string)) {
num3 = num1 * num2;
} else if (("/").equals(string)) {
num3 = num2 / num1;
} else {
throw new RuntimeException("运算符异常");
}
stack.push(String.valueOf(num3));
}
}
return Integer.parseInt(stack.pop());
}
}测试:
import java.util.List;
public class Test {
public static void main(String[] args) {
// (3+4)*5-6 -> 3 4 + 5 * 6 -
List<String> listString = PolandNotation.getListString("3 4 + 5 * 6 -");
int calculate = PolandNotation.calculate(listString);
System.out.println(calculate);
}
}
2.8中缀表达式->后缀表达式
中缀表达式“9+(3-1)×3+10÷2”转化为后缀表达式“9 3 1 - 3 * + 10 2 / +”。规则:从左到右遍历中缀表达式的每个数字和符号,若是数字就输出,即成为后缀表达式的一部分;若是符号,则判断其与栈顶符号的优先级,是右括号或优先级低于栈顶符号则栈顶元素依次出栈并输出,并将当前符号进栈,一直到最终输出后缀表达式为止。
思路:
初始化:创建
运算符栈和数栈(用于存储中间结果)从左至右扫描中缀表达式;
遇到操作数时,将其添加到
数栈中;遇到运算符时,比较其与
运算符栈顶运算符的优先级:
- 如果
运算符栈为空,则直接将此运算符入栈;- 如果优先级比栈顶运算符的高,将运算符压入
运算符栈;- 如果优先级比栈顶运算符的低或者等于,将运算符栈中的栈顶运算符弹出并追加到数栈中。
遇到括号时:
- 如果是左括号“(”,则直接压入运算符栈;
- 如果是右括号“)”,则依次弹出运算符栈顶的运算符,并追加到数栈中,直到遇到左括号为止,此时将这一对括号丢弃。
从左至右扫描中缀表达式结束后,将运算符栈中剩余的运算符依次追加到数栈中。
综上,可以发现数栈并没有出栈操作,并最后要逆序输出,所以用集合来代替。
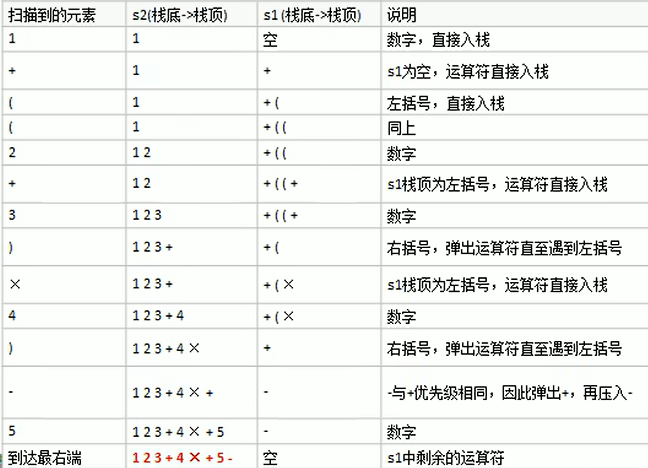
如下就是中缀表达式1+((2+3)*4)-5转换为后缀表达式的过程。
- BeforeToAfterExpression类
public List<String> beforeToAfterExpression(String expression):将中缀表达式转换为后缀表达式public int getPriority(String operation):返回运算符的优先级
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Stack;
public class BeforeToAfterExpression {
public List<String> beforeToAfterExpression(String expression) {
// 1.将字符串表达式转换为List结构
List<String> expressionList = Arrays.asList(expression.split(""));
// 2.创建符号栈
Stack charStack = new Stack();
// 3.创建集合用于存储数字和运算符
ArrayList<String> charList = new ArrayList<>();
for (String item : expressionList) {
if (item.matches("^\\d{1,}$")) {
// 4.如果是数字直接存入集合
charList.add(item);
} else if (("(").equals(item)) {
// 5.括号
// 5.1如果是左括号则直接入栈
charStack.push(item);
} else if ((")".equals(item))) {
// 5.2如果是右括号,则从符号栈中取出字符加入集合中,直到左括号为止
while (!("(").equals(charStack.peek())) {
charList.add(String.valueOf(charStack.pop()));
}
// 5.3删除左括号
charStack.pop();
} else {
// 6.运算符
// 6.1当当前运算符的优先级大于栈顶的优先级,则直接加入运算符栈
if (charStack.size() == 0 || (!("(").equals(charStack.peek()) && getPriority(item) > getPriority(String.valueOf(charStack.peek())))) {
charStack.push(item);
} else {
// 6.2当当前运算符的优先级小于于栈顶的优先级,则将栈顶元素出栈,并加入到集合当中,最后将当前字符入栈
while (charStack.size() != 0 && (!("(").equals(charStack.peek()) && getPriority(item) <= getPriority(String.valueOf(charStack.peek())))) {
charList.add(String.valueOf(charStack.pop()));
}
// 将当前操作的运算符入运算符栈
charStack.push(item);
}
}
}
// 7.将运算符栈中的所有元素加入集合
while (!charStack.empty()) {
charList.add(String.valueOf(charStack.pop()));
}
return charList;
}
/**
* 返回运算符的优先级
*
* @param operation 操作
* @return int
*/
public int getPriority(String operation) {
int priority = 0;
if (("+").equals(operation) || ("-").equals(operation)) {
priority = 1;
} else if (("*").equals(operation) || ("/").equals(operation)) {
priority = 2;
} else {
throw new RuntimeException("运算符错误");
}
return priority;
}
}- 测试
public class Test {
public static void main(String[] args) {
BeforeToAfterExpression beforeToAfterExpression = new BeforeToAfterExpression();
List<String> strings = beforeToAfterExpression.beforeToAfterExpression("1+((2+3)*4)-5");
System.out.println(strings);
}
}
3.递归
3.1递归概述
递归就是方法自己调用自己。每次调用时传入不同的变量。递归有助于编程者解决复杂的问题,同时可以让代码变得简洁。
3.2递归案例
打印问题:
JAVA
public static void test(int n) {
if (n > 2) {
test(n - 1);
}
System.out.println("n=" + n);
}阶乘问题:
JAVA
public static int factorial(int n) {
if (n == 1) {
return 1;
} else {
return factorial(n - 1) * n;
}
}3.3递归应用场景
- 各种数学问题如: 8皇后问题 , 汉诺塔, 阶乘问题, 迷宫问题, 球和篮子的问题(google编程大赛)
- 各种算法中也会使用到递归,比如快排,归并排序,二分查找,分治算法等
- 将用栈解决的问题使用递归代码比较简洁
3.4递归需要遵守的重要规则
- 执行一个方法时,就创建一个新的受保护的独立空间(栈空间)
- 方法的局部变量是独立的,不会相互影响
- 如果方法中使用的是引用类型变量(比如数组),就会共享该引用类型的数据
- 递归必须向退出递归的条件逼近,否则就是无限递归,出现
StackOverflowError异常- 当一个方法执行完毕,或者遇到return,就会返回,遵守谁调用,就将结果返回给谁,同时当方法执行完毕或者返回时,该方法也就执行完毕。
3.5回溯(Backtrack)
3.5.1介绍
回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法。
3.5.2回溯和递归的区别
递归是一种算法结构。递归会出现在子程序中,形式上表现为直接或间接的自己调用自己。
回溯是一种算法思想。它是用递归实现的。回溯的过程类似于穷举法,但回溯有“剪枝”功能,即自我判断过程。例如有求和问题,给定有 7 个元素的组合 [1, 2, 3, 4, 5, 6, 7],求加和为 7 的子集。累加计算中,选择 1+2+3+4 时,判断得到结果为 10 大于 7,那么后面的 5, 6, 7 就没有必要计算了。这种方法属于搜索过程中的优化,即“剪枝”功能。
用一个比较通俗的说法来解释递归和回溯:
我们在路上走着,前面是一个多岔路口,因为我们并不知道应该走哪条路,所以我们需要尝试。尝试的过程就是一个函数。
我们选择了一个方向,后来发现又有一个多岔路口,这时候又需要进行一次选择。所以我们需要在上一次尝试结果的基础上,再做一次尝试,即在函数内部再调用一次函数,这就是递归的过程。
这样重复了若干次之后,发现这次选择的这条路走不通,这时候我们知道我们上一个路口选错了,所以我们要回到上一个路口重新选择其他路,这就是回溯的思想。
3.5.3迷宫问题
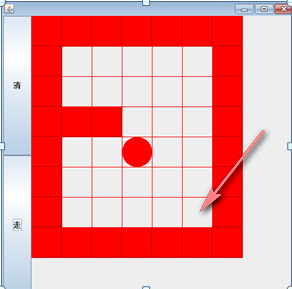
- 小球得到的路径,和程序员设置的找路策略有关即:找路的上下左右的顺序相关
- 再得到小球路径时,可以先使用(下右上左),再改成(上右下左),看看路径是不是有变化
public class MiGong {
public static void runGame() {
int[][] miGong = new int[8][7];
// 第一行和最后一行置为1(列变)
for (int i = 0; i < 7; i++) {
miGong[0][i] = miGong[7][i] = 1;
// 设置第3行的第3列为1
if (i == 2){
miGong[i][i] = 1;
}
// 设置第4行的第2列和第3列为1
if (i == 3) {
miGong[i][1] = miGong[i][2] = 1;
}
}
// 第一列和最后一列置为1(行变)
for (int i = 0; i < 8; i++) {
miGong[i][0] = miGong[i][6] = 1;
}
for (int i = 0; i < miGong.length; i++) {
for (int j = 0; j < miGong[i].length; j++) {
System.out.print(miGong[i][j] + " ");
}
System.out.println();
}
boolean result = setWay(miGong, 1, 1);
System.out.println("-----------------");
System.out.println(result);
System.out.println("-----------------");
for (int i = 0; i < miGong.length; i++) {
for (int j = 0; j < miGong[i].length; j++) {
System.out.print(miGong[i][j] + " ");
}
System.out.println();
}
}
/**
* 设置方法
*
* @param map 地图
* @param i 从哪个位置开始找
* @param j // 使用递归回溯来给小球找路
* // 1. map 表示地图
* // 2. i,j 表示从地图的哪个位置开始出发 (1,1)
* // 3. 如果小球能到 map[6][5] 位置,则说明通路找到.
* // 4. 约定: 当map[i][j] 为 0 表示该点没有走过;为 1 表示墙 ; 2 表示走过,是通路 ; 3 表示该点已经走过,但是走不通
* // 5. 在走迷宫时,需要确定一个策略(方法) 下->右->上->左 , 如果该点走不通,再回溯
* @return boolean
*/
public static boolean setWay(int[][] map, int i, int j) {
// 下标6,5(第7行第6列)就表示到达终点
if (map[6][5] == 2) {
return true;
} else {
if (map[i][j] == 0) {
// 如果该点可以走通,则将其标记为2
map[i][j] = 2;
if (setWay(map, i + 1, j)) { //向下走
return true;
} else if (setWay(map, i, j + 1)) { //向右走
return true;
} else if (setWay(map, i - 1, j)) { //向上走
return true;
} else if (setWay(map, i, j - 1)) { //向左走
return true;
} else {
// 该点走不通
map[i][j] = 3;
return false;
}
} else { //为 1 表示墙 ; 2 表示走过,是通路 ; 3 表示该点已经走过,但是走不通
return false;
}
}
}
public static void main(String[] args) {
MiGong.runGame();
}
}测试结果:
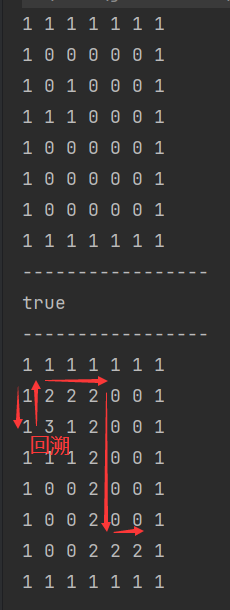
3.5.4八皇后问题

3.5.4.1说明
八皇后问题,是一个古老而著名的问题,是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出:在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即:任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
3.5.4.2思路分析
- 第一个皇后先放第一行第一列
- 第二个皇后放在第二行第一列、然后判断是否OK, 如果不OK,继续放在第二列、第三列、依次把所有列都放完,找到一个合适
- 继续第三个皇后,还是第一列、第二列……直到第8个皇后也能放在一个不冲突的位置,就算是找到了一个正确解
- 当得到一个正确解时,栈回退到上一个栈时,就会开始回溯,即将第一个皇后,放到第一列的所有正确解,全部得到.
- 然后回头继续第一个皇后放第二列,后面继续循环执行 1,2,3,4的步骤
public class Queen {
private static final int max = 8;
// 使用一维数组,定义8个元素表示8个皇后,下标就表示皇后的序号。元素就表示当前皇后所处的列。
private static int[] array = new int[max];
private static int count = 0;
public static void runGame() {
// 放置第一个皇后
pushQueen(0);
}
/**
* 放置第n个皇后
* 特别注意: pushQueen 是每一次递归时,进入到check中都有for(int i = 0; i < max; i++), 因此会有回溯
*
* @param n n
*/
private static void pushQueen(int n) {
if (n == max) {
print();
return;
}
for (int i = 0; i < max; i++) {
// 把第n个皇后放到该行第一列
array[n] = i;
// 判断是否冲突
if (judge(n)) {
pushQueen(n + 1);
}
// 如果冲突,就继续执行array[n] = i;即将第n个皇后,放置在本行得后移的一个位置
}
}
/**
* 查看当我们放置第n个皇后,就去检测该皇后是否和前面已经摆放的皇后冲突
*
* @param n n表示第n个皇后
* @return boolean
*/
private static boolean judge(int n) {
for (int i = 0; i < n; i++) {
// array[i] == array[n]:判断当前皇后是否和数组中已经存在的皇后在同一列
// Math.abs(n - i) == Math.abs(array[n] - array[i]):表示判断第n个皇后是否和第i皇后是否在同一斜线
// 判断行与列的差的绝对值是否相等,相等则在同一条直线
if (array[i] == array[n] || Math.abs(n - i) == Math.abs(array[n] - array[i])) {
return false;
}
}
return true;
}
/**
* 打印
*/
public static void print() {
count++;
for (int i = 0; i < array.length; i++) {
System.out.print(i + " ");
}
System.out.println();
}
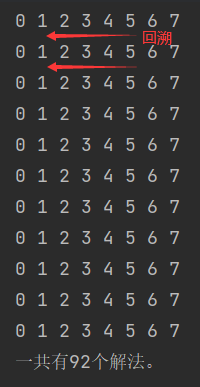
public static void main(String[] args) {
Queen.runGame();
System.out.println("一共有" + count + "个解法。");
}
}
4.排序
4.1排序的介绍
排序也称排序算法(Sort Algorithm),排序是将一组数据,依指定的顺序进行排列的过程。
4.2排序的分类
- 按照存储位置分类
内排序是在排序整个过程中,待排序的所有记录全部被放置在内存中。
外排序是由于排序的记录个数太多,不能同时放置在内存,整个排序过程需要在内外存之间多次交换数据才能进行。
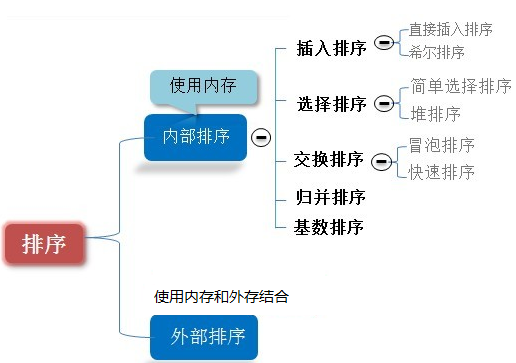
- 按照是否进行元素比较进行分类
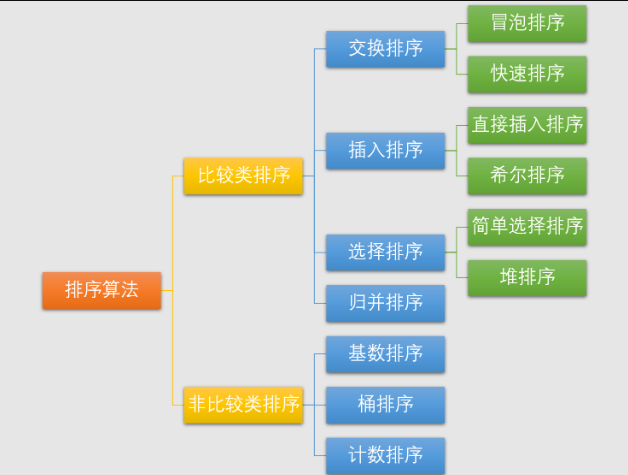
常见的快速排序、归并排序、堆排序以及冒泡排序等都属于比较类排序算法。比较类排序是通过比较来决定元素间的相对次序,由于其时间复杂度不能突破 O(nlogn),因此也称为非线性时间比较类排序。在冒泡排序之类的排序中,问题规模为 n,又因为需要比较 n 次,所以平均时间复杂度为 O(n²)。在归并排序、快速排序之类的排序中,问题规模通过分治法消减为 logn 次,所以时间复杂度平均 O(nlogn)。
比较类排序的优势是,适用于各种规模的数据,也不在乎数据的分布,都能进行排序。可以说,比较排序适用于一切需要排序的情况。
而计数排序、基数排序、桶排序则属于非比较类排序算法。非比较排序不通过比较来决定元素间的相对次序,而是通过确定每个元素之前,应该有多少个元素来排序。由于它可以突破基于比较排序的时间下界,以线性时间运行,因此称为线性时间非比较类排序。 非比较排序只要确定每个元素之前的已有的元素个数即可,所有一次遍历即可解决。算法时间复杂度 O(n)。
非比较排序时间复杂度底,但由于非比较排序需要占用空间来确定唯一位置。所以对数据规模和数据分布有一定的要求。
4.3算法的时间复杂度
4.3.1算法效率的度量方法
事后统计方法:这种方法主要是通过设计好的测试程序和数据,利用计算机计时器对不同算法编制的程序的运行时间进行比较,从而确定算法效率的高低。
缺陷:
- 必须依据算法事先编制好程序,这通常需要花费大量的时间和精力。
- 时间的比较依赖计算机硬件和软件等环境因素,有时会掩盖算法本身的优劣。
- 算法的测试数据设计困难,并且程序的运行时间往往还与测试数据的规模有很大关系,效率高的算法在小的测试数据面前往往得不到体现。
事前分析估算方法:通过分析某个算法的时间复杂度来判断哪个算法更优。
4.3.2时间复杂度的定义
时间复杂度是一个概念,它用来描述算法运行时间随着输入数据量增长的变化趋势。它通常用大O符号表示,表示算法运行时间的上界。这样用大写O()来体现算法时间复杂度的记法,我们称之为大O记法。
一般情况下,随着n的增大,T(n)增长最慢的算法为最优算法。
T(n) 不同,但时间复杂度可能相同。 如:T(n)=n²+7n+6 与 T(n)=3n²+2n+2 它们的T(n) 不同,但时间复杂度相同,都为O(n²)。
4.3.3计算时间复杂度的方法
保留最高阶,并除去最高阶的系数。
- 用常数1代替运行时间中的所有加法常数 T(n)=n²+7n+6 => T(n)=n²+7n+1
- 修改后的运行次数函数中,只保留最高阶项 T(n)=n²+7n+1 => T(n) = n²
- 如果最高阶项存在且不是1,则去除与这个项相乘的常数。
得到的结果就是大O阶。 T(n)=2n² => T(n) = n²=> O(n²)
4.3.4常见的时间复杂度
- 常数阶O(1)
- 对数阶O(log2n)
- 线性阶O(n)
- 线性对数阶O(nlog2n)
- 平方阶O(n^2)
- 立方阶O(n^3)
- k次方阶O(n^k)
- 指数阶O(2^n)
常见的算法时间复杂度由小到大依次为:Ο(1)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n^2)<Ο(n^3)< Ο(n^k) <Ο(2^n) ,随着问题规模n的不断增大,上述时间复杂度不断增大,算法的执行效率越低。
4.3.4.1常数阶O(1)
无论代码执行了多少行,只要是没有循环等复杂结构,那这个代码的时间复杂度就都是O(1)
int i = 1;
int j = 2;
j++;
i++;
int m = i + j;说明:上述代码在执行的时候,它消耗的时间并不随着某个变量的增长而增长,那么无论这类代码有多长,即使有几万几十万行,都可以用O(1)来表示它的时间复杂度。
4.3.4.2对数阶O(log2n)
int i = 1;
while(i<n){
i = i * 2 ;
}说明:在while循环里面,每次都将 i 乘以 2,乘完之后,i 距离 n 就越来越近了。假设循环x次之后,i 就大于 n 了,此时这个循环就退出了,也就是说 2 的 x 次方等于 n,那么 x =log2n也就是说当循环 log2n 次以后,这个代码就结束了。因此这个代码的时间复杂度为:O(log2n) 。 O((log2n) 的这个2 时间上是根据代码变化的,i = i * 3时 ,则是 O((log3n) 。
如果N=a^x(a>0,a≠1),即a的x次方等于N(a>0,且a≠1),那么数x叫做以a为底N的对数(logarIthm),记作x=logaN。其中,a叫做对数的底数,N叫做真数,x叫做以a为底N的对数。
4.3.4.3线性阶O(n)
for(int i = 0; i<=n; i++){
j = i;
j++;
}说明:这段代码,for循环里面的代码会执行n遍,因此它消耗的时间是随着n的变化而变化的,因此这类代码都可以用O(n)来表示它的时间复杂度
4.3.4.4线性对数阶O(nlogN)
for(int m = 1; m<=n; m++){
i = 1;
int i = 1;
while(i<n){
i = i * 2 ;
}
}说明:线性对数阶O(nlogN) 其实非常容易理解,将时间复杂度为O(logn)的代码循环N遍的话,那么它的时间复杂度就是 n * O(logN),也就是了O(nlogN)
4.3.4.5平方阶O(n²)
for(int x = 1; x<=n; x++){
for(int i = 1; i<=n; i++){
j = i;
j++;
}
}说明:平方阶O(n²) 就更容易理解了,如果把 O(n) 的代码再嵌套循环一遍,它的时间复杂度就是 O(n²),这段代码其实就是嵌套了2层n循环,它的时间复杂度就是 O(n x n),即 O(n²)。 如果将其中一层循环的n改成m,那它的时间复杂度就变成了 O(m x n)
4.4平均时间复杂度和最坏时间复杂度
- 平均时间复杂度是指所有可能的输入实例均以等概率出现的情况下,该算法的运行时间。
- 最坏情况下的时间复杂度称最坏时间复杂度。一般讨论的时间复杂度均是最坏情况下的时间复杂度。 这样做的原因是:最坏情况下的时间复杂度是算法在任何输入实例上运行时间的界限,这就保证了算法的运行时间不会比最坏情况更长。
- 平均时间复杂度和最坏时间复杂度是否一致,和算法有关。
| 排序算法 | 时间复杂度(最好) | 时间复杂度(最坏) | 时间复杂度(平均) | 空间复杂度 | 排序方式 | 稳定性 |
|---|---|---|---|---|---|---|
| 冒泡排序 | O(n) | O(n^2) | O(n^2) | O(1) | In-place | 稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | In-place | 不稳定 |
| 插入排序 | O(n) | O(n^2) | O(n^2) | O(1) | In-place | 稳定 |
| 希尔排序 | O(n logn) | O(n^2) | O(n logn) | O(1) | In-place | 不稳定 |
| 归并排序 | O(n logn) | O(n logn) | O(n logn) | O(n) | Out-place | 稳定 |
| 快速排序 | O(n logn) | O(n logn) | O(n logn) | O(logn) | In-place | 不稳定 |
| 堆排序 | O(n logn) | O(n logn) | O(n logn) | O(1) | In-place | 不稳定 |
| 计数排序 | O(n+k) | O(n+k) | O(n+k) | O(k) | Out-place | 稳定 |
| 桶排序 | O(n+k) | O(n^2) | O(n+k) | O(n+k) | Out-place | 稳定 |
| 基数排序 | O(n*k) | O(n*k) | O(n*k) | O(n+k) | Out-place | 稳定 |
4.5算法的空间复杂度
- 类似于时间复杂度的讨论,一个算法的空间复杂度(Space Complexity)定义为该算法所耗费的存储空间,它也是问题规模n的函数。
- 空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度。有的算法需要占用的临时工作单元数与解决问题的规模n有关,它随着n的增大而增大,当n较大时,将占用较多的存储单元,例如快速排序和归并排序算法就属于这种情况。
- 在做算法分析时,主要讨论的是
时间复杂度。从用户使用体验上看,更看重的程序执行的速度。一些缓存产品(redis, memcache)和算法(基数排序)本质就是用空间换时间。
4.6冒泡排序 (Bubble Sort)
4.6.1概念
冒泡排序是一种简单的排序算法。它重复地遍历要排序的序列,依次比较两个元素,如果它们的顺序错误就把它们交换过来。遍历序列的工作是重复地进行直到没有再需要交换为止,此时说明该序列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢 “浮” 到数列的顶端。
4.6.2算法步骤
- 比较相邻的元素。如果第一个比第二个大,就交换它们两个;
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
- 针对所有的元素重复以上的步骤,除了最后一个;
- 重复步骤 1~3,直到排序完成。
4.6.3图解算法
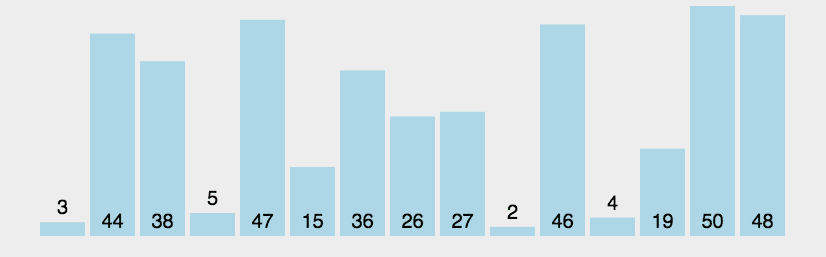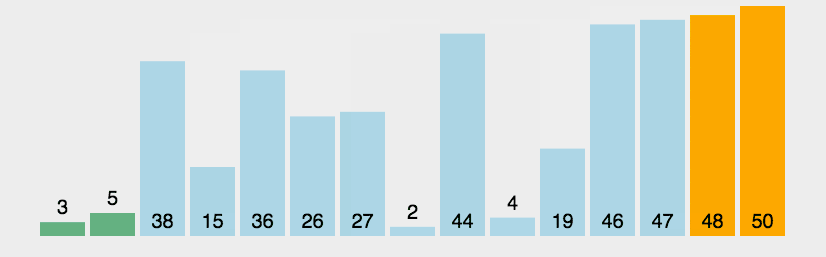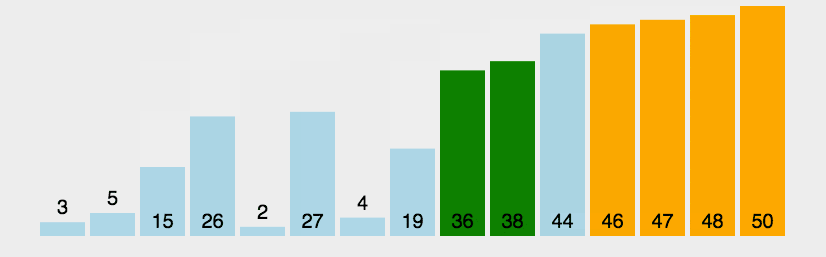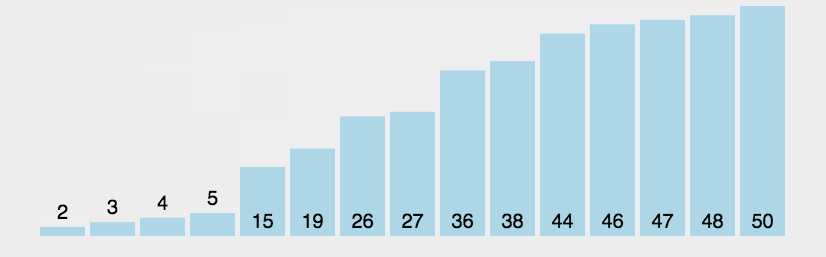
4.6.3算法分析
- 稳定性:稳定
- 时间复杂度:最佳:O(n) ,最差:O(n2), 平均:O(n2)
- 空间复杂度:O(1)
- 排序方式:In-place
4.6.4算法实现
- 外层循环控制排序的趟数。
- 内层循环控制每趟比较的次数,在内层循环中比较相邻元素得大小。
- 内层循环每结束一次,则得将未排序中得最大值放到排好序元素得最前面。
此处对代码做了优化,加入了 flog 用于标识本次排序是否发生交换,如果未发生交换,则表示当前趟数已经完成排序。即当原输入序列就是排序好的情况下,该算法的时间复杂度就是 O(n)。
public class BubbleSort {
public static void main(String[] args) {
bubbleSort(new int[]{5, 2, 8, 3, 4, 7, 9, 10, 1, 6});
}
/**
* 冒泡排序
*
* @param numbers 数字
*/
public static void bubbleSort(int[] numbers) {
// 外层循环控制排序趟数
for (int i = 0; i < numbers.length - 1; i++) {
// 定义标识,如果为true,说明没有发生交换,排序完成
boolean flog = false;
// 内层循环控制每一趟排序多少次
// 每一趟排序都会把最大的数放到最后,所以每一趟排序次数都会减少,减少的次数就是i
for (int j = 0; j < numbers.length - i - 1; j++) {
if (numbers[j] > numbers[j + 1]) {
int temp = numbers[j];
numbers[j] = numbers[j + 1];
numbers[j + 1] = temp;
// 如果发生交换,则将标识改为true
flog = true;
}
}
// 如果此次排序没有发生交换,说明排序完成,直接跳出循环,排序完成
if (!flog) {
break;
}
}
for (int number : numbers) {
System.out.print(number + " ");
}
}
}4.7选择排序 (Selection Sort)
4.7.1概述
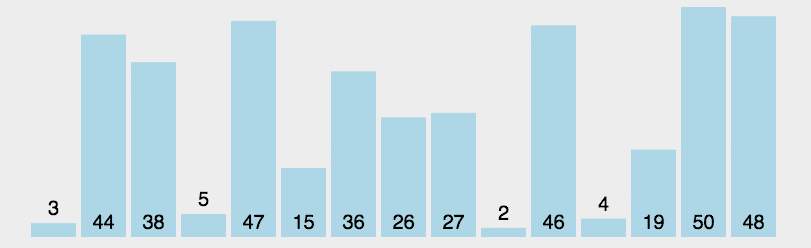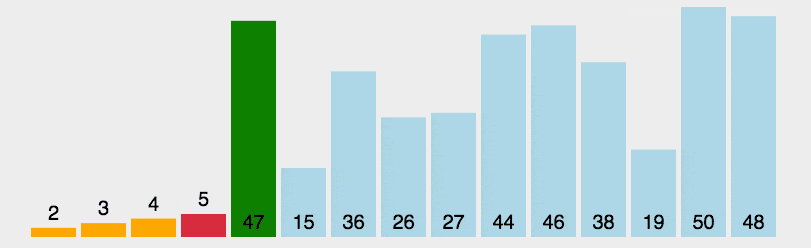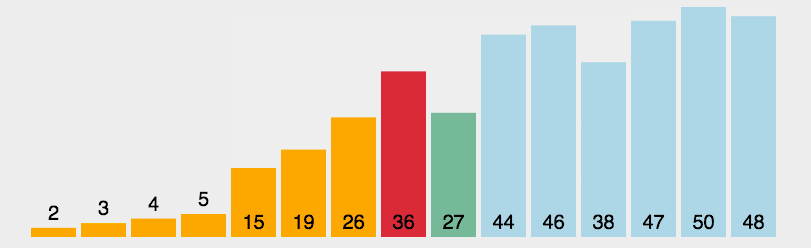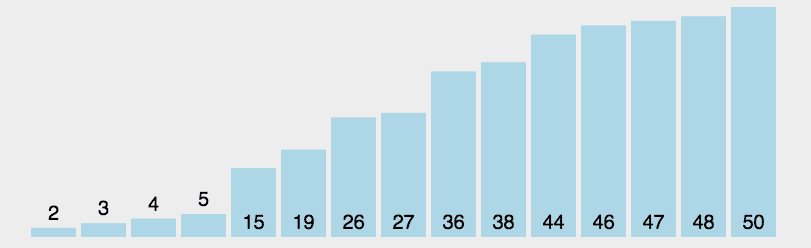
选择排序首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
选择排序是一种简单直观的排序算法,无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间。
4.7.2算法步骤
- 首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置
- 再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
- 重复第 2 步,直到所有元素均排序完毕。
4.7.3图解算法
4.7.4算法分析
- 稳定性:不稳定
- 时间复杂度:最佳:O(n2) ,最差:O(n2), 平均:O(n2)
- 空间复杂度:O(1)
- 排序方式:In-place
4.7.5代码实现
- 外层循环控制排序趟数,将最小元素的下标设置为当前元素
- 内层循环控制每趟比较次数,以当前元素得下标为minIdex,比较是否存在比minIndex下标元素更小的元素,如果存在,则将minIndex设置为当前元素的下标。
- 内存循环结束后,判断minIndex是否等于i,如果等于,则表示没有比当前元素更小的。如果不等于,则表明存在比当前下标i更小的元素,则交换元素位置。
public class SelectionSort {
public static void main(String[] args) {
selectionSort(new int[]{5, 2, 8, 3, 4, 7, 9, 10, 1, 6});
}
public static void selectionSort(int[] numbers) {
// 外层循环控制排序趟数
for (int i = 0; i < numbers.length - 1; i++) {
// 将当前下标定义为最小值下标
int mixIndex = i;
// 内层循环控制比较次数
for (int j = i; j < numbers.length; j++) {
// 如果存在比当前最小值小的数,将此数的下标赋值给mixIndex
if (numbers[j] < numbers[mixIndex]) {
mixIndex = j;
}
}
// 内层循环比较完成后,判断当前i是否等于minIndex,
// 如果等于,说明当前数就是最小值,不需要交换
// 如果不等于,说明存在比当前数更小的值,需要交换
if (mixIndex != i) {
int temp = numbers[i];
numbers[i] = numbers[mixIndex];
numbers[mixIndex] = temp;
}
}
for (int number : numbers) {
System.out.print(number + " ");
}
}
}4.8插入排序 (Insertion Sort)
4.8.1插入排序的概念
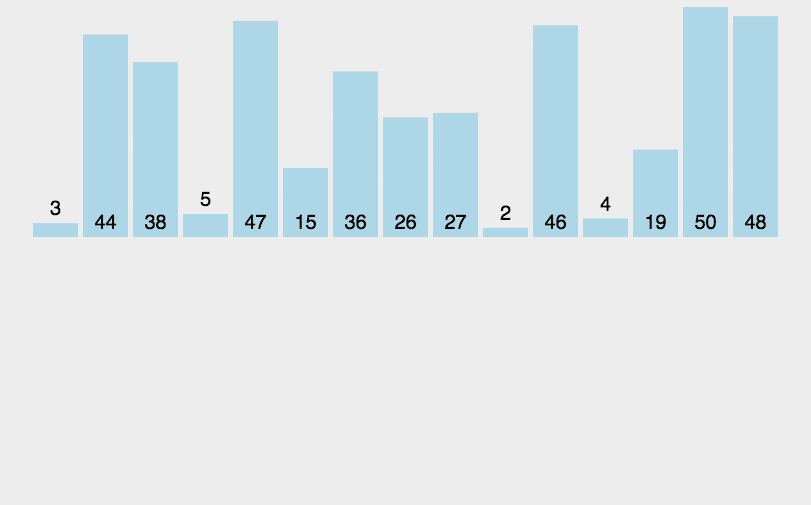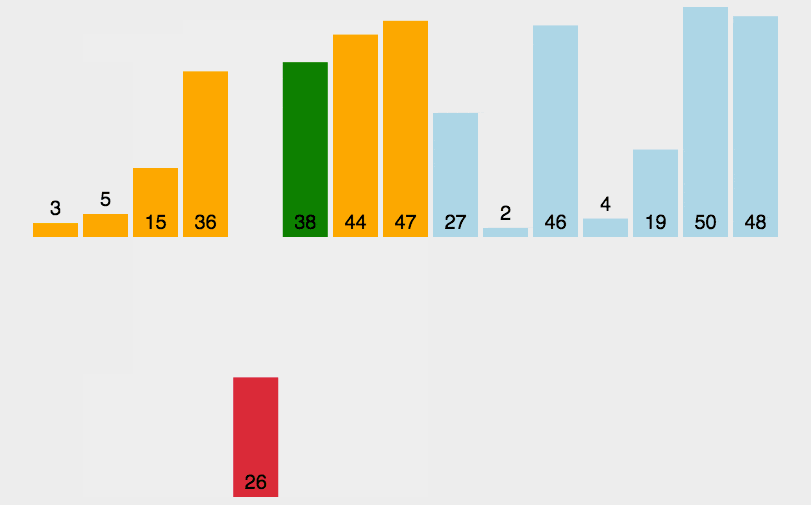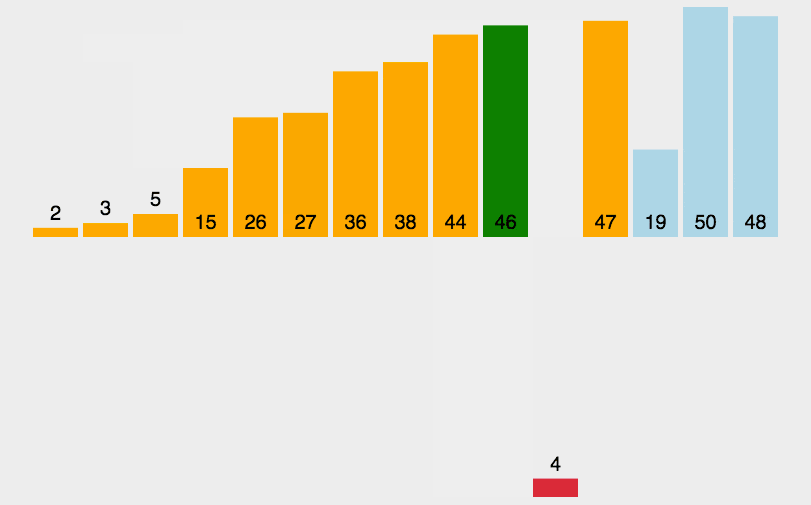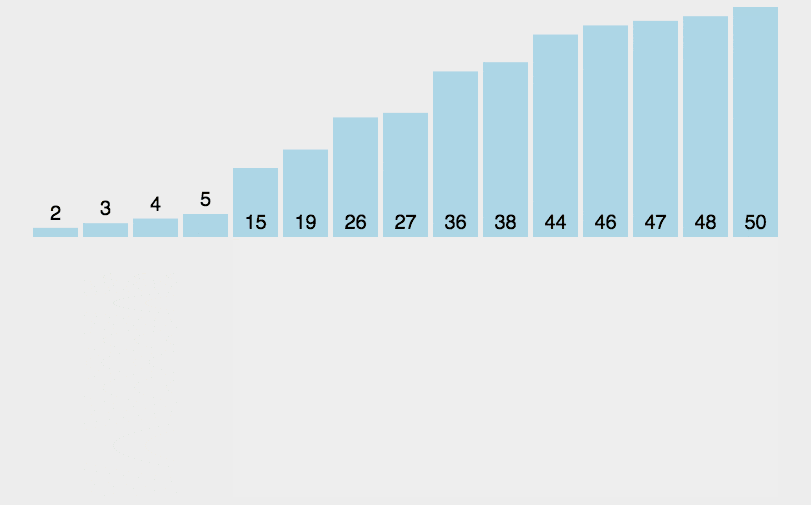
插入排序是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入该数据。插入排序在实现上,通常采用 in-place 排序(即只需用到 O(1) 的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
插入排序和冒泡排序一样,也有一种优化算法,叫做拆半插入。
4.8.2算法步骤
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 重复步骤 3,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置后;
- 重复步骤 2~5。
4.8.3图解算法
4.8.4算法分析
- 稳定性:稳定
- 时间复杂度:最佳:O(n) ,最差:O(n2), 平均:O(n2)
- 空间复杂度:O(1)
- 排序方式:In-place
4.8.5代码实现
- 在外层循环中控制比较的趟数。
- preIndex表示前一个数的下标,current就表示当前数,就是比较当前数和前一个数的大小
- while循环中,判断当前数是否小于前一个数,如果小于,则将前一个数后移,循环操作,直到当前数大于等于前一个数。
- 最后将当前数插入到前一个数的后面
public class InsertionSort {
public static void main(String[] args) {
insertionSort(new int[]{5, 2, 8, 3, 4, 7, 9, 10, 1, 6});
}
/**
* 插入排序
*
* @param numbers 数字
*/
public static void insertionSort(int[] numbers) {
// 外层循环控制排序趟数,从第二个数开始,因为第一个数默认是有序的
for (int i = 1; i < numbers.length; i++) {
// 定义当前数的前一个数的下标,目的是为了方便后面的比较
int preIndex = i - 1;
// 定义当前数
int current = numbers[i];
// 如果当前数比前一个数小,就将前一个数后移一位,直到当前数大于等于前一个数
while (preIndex >= 0 && current < numbers[preIndex]) {
// 将前一个数后移一位
numbers[preIndex + 1] = numbers[preIndex];
// 下标前移一位
preIndex = preIndex - 1;
}
// 将当前数插入到前一个数的后面
numbers[preIndex + 1] = current;
}
for (int number : numbers) {
System.out.print(number + " ");
}
}
}4.9希尔排序(Donald Shell Sort)
4.9.1概念
希尔排序是希尔 (Donald Shell) 于 1959 年提出的一种排序算法。希尔排序也是一种插入排序,它是简单插入排序经过改进之后的一个更高效的版本,也称为递减增量排序算法,同时该算法是冲破 O(n²) 的第一批算法之一。
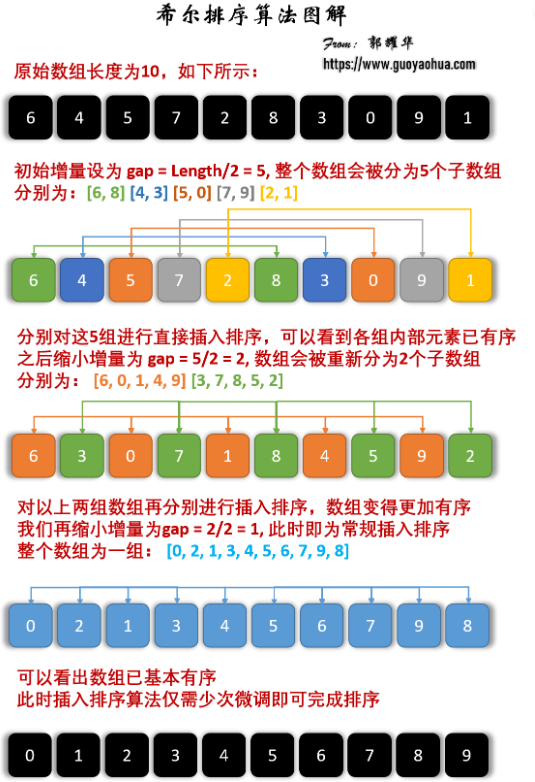
希尔排序的基本思想是:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录 “基本有序” 时,再对全体记录进行插入排序。
4.9.2算法步骤
我们来看下希尔排序的基本步骤,在此我们选择增量 gap=length/2,缩小增量继续以 gap = gap/2 的方式,这种增量选择我们可以用一个序列来表示,{n/2, (n/2)/2, ..., 1},称为增量序列。希尔排序的增量序列的选择与证明是个数学难题,我们选择的这个增量序列是比较常用的,也是希尔建议的增量,称为希尔增量,但其实这个增量序列不是最优的。此处我们做示例使用希尔增量。
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,具体算法描述:
- 选择一个增量序列
{t1, t2, …, tk},其中(ti>tj, i<j, tk=1);- 按增量序列个数 k,对序列进行 k 趟排序;
- 每趟排序,根据对应的增量
t,将待排序列分割成若干长度为m的子序列,分别对各子表进行直接插入排序。仅增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
4.9.3图解算法
4.9.4算法分析
- 稳定性:不稳定
- 时间复杂度:最佳:O(nlogn), 最差:O(n^2) 平均:O(nlogn)
- 空间复杂度:
O(1)
4.9.5算法实现
- 希尔排序就是特殊的插入排序,其本质也是基于插入排序实现的
- 需要定义增量
public class DonaldShellSort {
public static void main(String[] args) {
donaldShellSort(new int[]{5, 2, 8, 3, 4, 7, 9, 10, 1, 6});
}
public static void donaldShellSort(int[] nums) {
// 1.定义初始增量
int gap = nums.length / 2;
//当增量为0时,表示对所有元素进行了一次插入排序
while (gap > 0) {
// 2.外层循环控制比较的趟数
for (int i = gap; i < nums.length; i++) {
// 3.定义前一个数
int preIndex = i - gap;
// 4.定义当前数
int current = nums[i];
// 5.判断当前数是否大于等于前一个数,不大于等于那就前一个数后移,并重新定义前一个数的preIndex
while (preIndex >= 0 && nums[preIndex] > current) {
// 6.将前一个数后移gap位
nums[preIndex + gap] = nums[preIndex];
// 7.下标前移gap位
preIndex = preIndex - gap;
}
nums[preIndex + gap] = current;
}
// 每次趟数结束就表明已经完成了一次插入排序,重新定义增量
gap /= 2;
}
for (int num : nums) {
System.out.print(num + " ");
}
}
}4.10归并排序(Merge Sort)
4.10.1概述
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法 (Divide and Conquer) 的一个非常典型的应用。归并排序是一种稳定的排序方法。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。
4.10.2算法步骤
归并排序算法是一个递归过程,边界条件为当输入序列仅有一个元素时,直接返回,具体过程如下:
- 如果输入内只有一个元素,则直接返回,否则将长度为
n的输入序列分成两个长度为n/2的子序列;- 分别对这两个子序列进行归并排序,使子序列变为有序状态;
- 设定两个指针,分别指向两个已经排序子序列的起始位置;
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间(用于存放排序结果),并移动指针到下一位置;
- 重复步骤 3 ~4 直到某一指针达到序列尾;
- 将另一序列剩下的所有元素直接复制到合并序列尾。
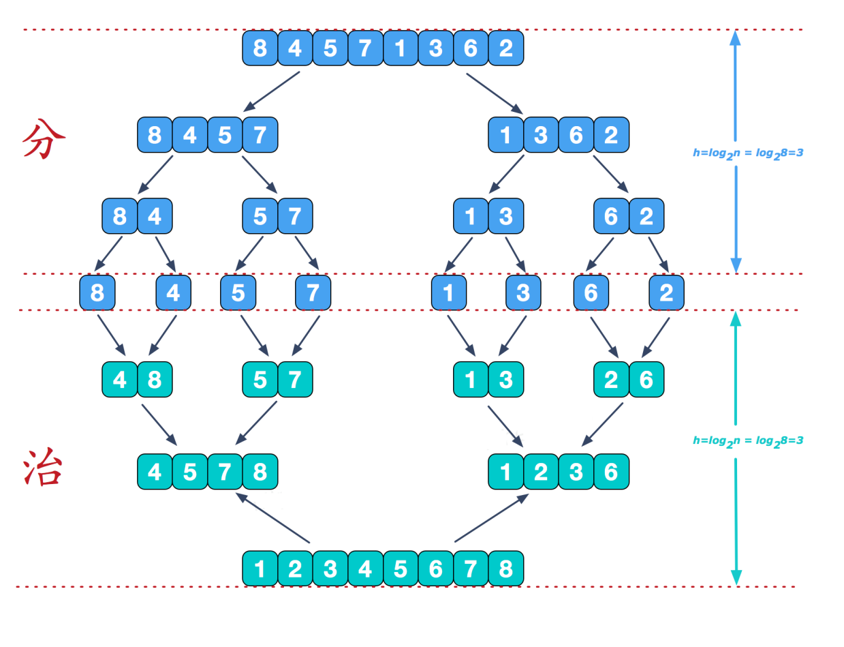
分阶段可以理解为就是递归拆分子序列的过程。
再来看看治阶段,我们需要将两个已经有序的子序列合并成一个有序序列,比如上图中的最后一次合并,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],来看下实现步骤:
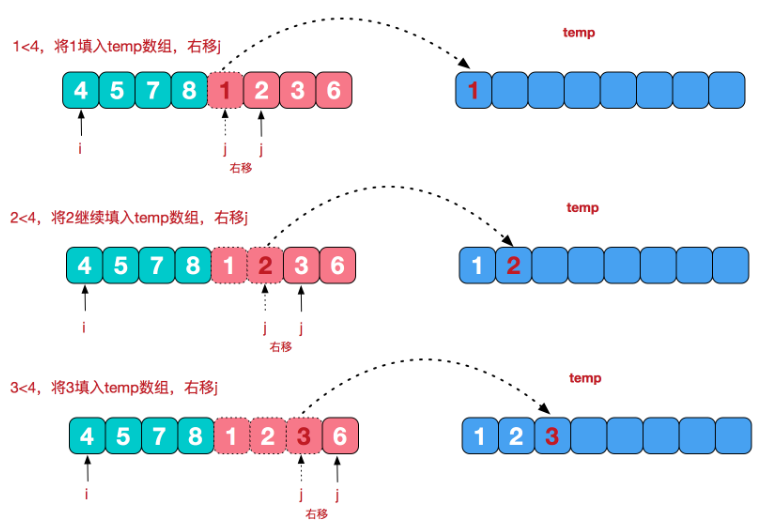
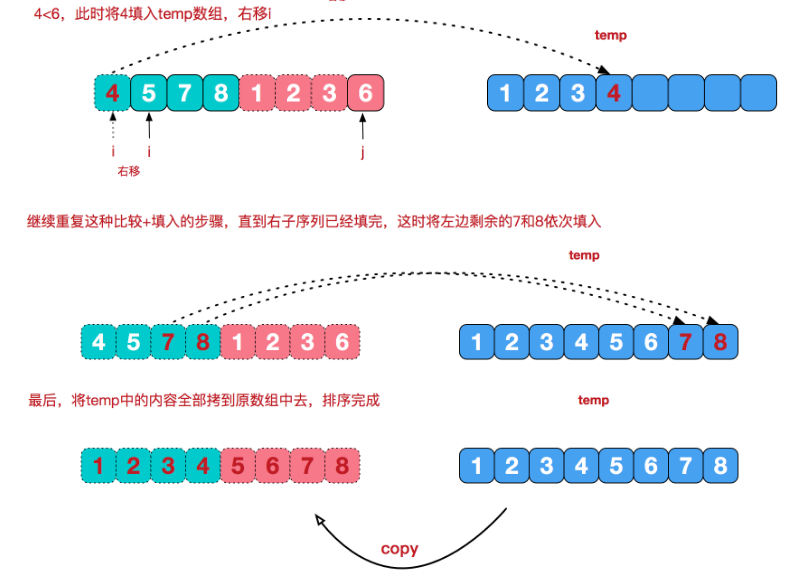
4.10.3图解算法
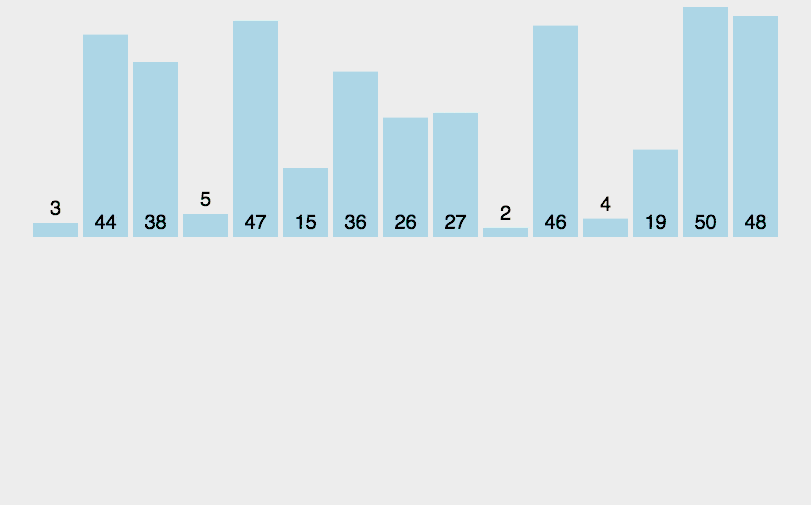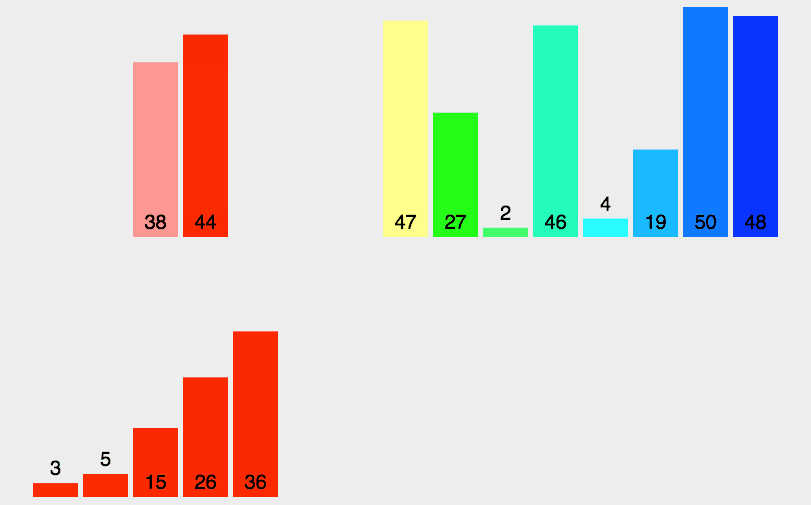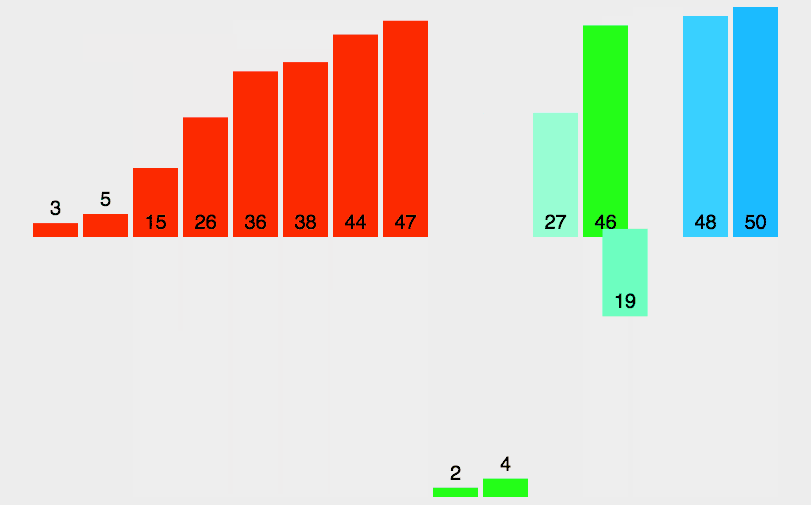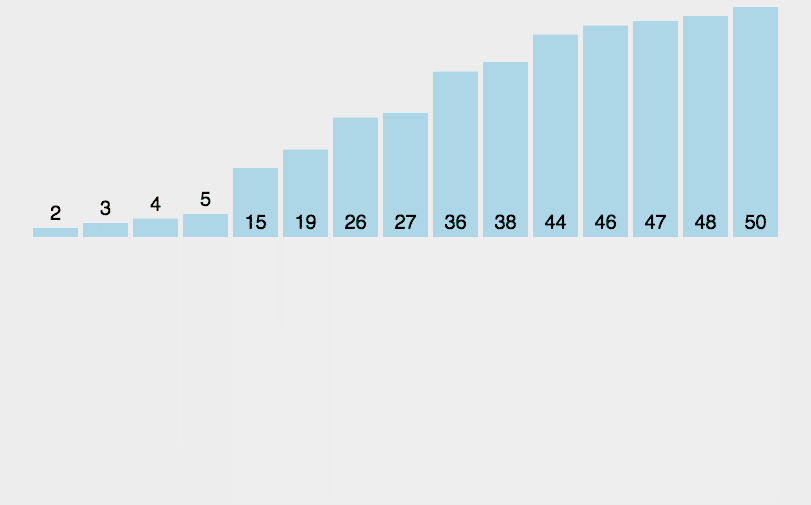
4.10.4算法分析
- 稳定性:稳定
- 时间复杂度:最佳:O(nlogn), 最差:O(nlogn), 平均:O(nlogn)
- 空间复杂度:O(n)
4.10.5代码实现
import java.util.Arrays;
public class MergeSort {
public static void main(String[] args) {
int[] nums = {5, 2, 8, 3, 4, 7, 9, 10, 1, 6};
mergeSort(nums, 0, nums.length - 1);
System.out.println(Arrays.toString(nums));
}
public static void mergeSort(int nums[], int left, int right) {
if (left < right) {
// 将长度为 `n` 的输入序列分成两个长度为 `n/2` 的子序列
int mid = (left + right) / 2;
// 向左递归分解
mergeSort(nums, left, mid);
// 向右递归分解
mergeSort(nums, mid + 1, right);
// 合并
merge(nums, left, mid, right);
}
}
/**
* 归并排序
*
* @param nums 排序的原始数组
* @param left 左边有序序列的初始索引
* @param mid 中间索引
* @param right 右边索引
*/
public static void merge(int nums[], int left, int mid, int right) {
// 初始化i,表示左边有序序列的初始索引
int i = left;
// 初始化j,表示右边有序序列的初始索引
int j = mid + 1;
// 临时数组temp的当前索引
int[] temp = new int[right - left + 1];
int t = 0;
// 把左右两个有序数据按照规则填充到temp,直到左右两个有序序列一边处理完毕为止
while (i <= mid && j <= right) {
// 如果左边有序序列的当前元素小于等于右边有序序列的当前元素,就将左边有序序列的当前元素添加到temp数组。
if (nums[i] <= nums[j]) {
temp[t++] = nums[i++];
} else {
// 如果右边有序序列的当前元素小于等于右边有序序列的当前元素,就将右边有序序列的当前元素添加到temp数组。
temp[t++] = nums[j++];
}
}
// 将剩余一边的有序序列添加到temp
// 如果左边元素有剩余
while (i <= mid) {
temp[t++] = nums[i++];
}
// 如果右边元素有剩余
while (j <= right) {
temp[t++] = nums[j++];
}
// 将临时数组temp的元素重新拷贝到nums
for (int k = 0; k < t; k++) {
nums[left++] = temp[k];
}
}
}
4.11快速排序(Quick Sort)
4.11.1概念
快速排序用到了分治思想,同样的还有归并排序。乍看起来快速排序和归并排序非常相似,都是将问题变小,先排序子串,最后合并。不同的是快速排序在划分子问题的时候经过多一步处理,将划分的两组数据划分为一大一小,这样在最后合并的时候就不必像归并排序那样再进行比较。但也正因为如此,划分的不定性使得快速排序的时间复杂度并不稳定。
快速排序的基本思想:通过一趟排序将待排序列分隔成独立的两部分,其中一部分记录的元素均比另一部分的元素小,则可分别对这两部分子序列继续进行排序,以达到整个序列有序。
4.11.2算法步骤
快速排序使用分治法open in new window(Divide and conquer)策略来把一个序列分为较小和较大的 2 个子序列,然后递回地排序两个子序列。具体算法描述如下:
- 从序列中随机挑出一个元素,做为 “基准”(
pivot);- 重新排列序列,将所有比基准值小的元素摆放在基准前面,所有比基准值大的摆在基准的后面。在这个操作结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 递归地把小于基准值元素的子序列和大于基准值元素的子序列进行快速排序font>
4.11.3图解算法
- 选择基准值
选择不同位置的基准值,快速排序就有不同的变体。下面以最后一个元素作为基准值。

- 重新排列数组
现在重新排列数组,将比基准值小的放在左边,比基准值大的放在右边。
指针固定在基准值上,将基准值与从第一个索引开始的元素进行比较。
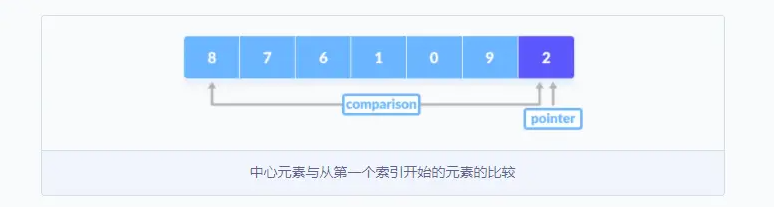
- 如果该元素大于基准值,则为该元素设置第二指针。
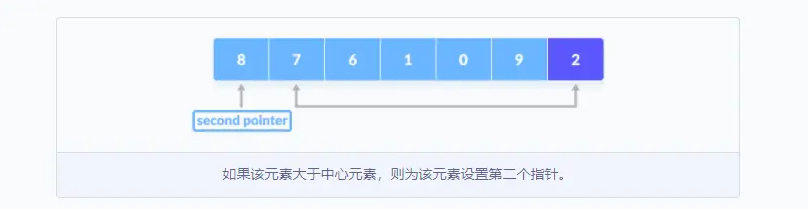
- 现在将基准值与其他元素进行比较,如果到达的元素小于基准值,则将较小的元素和上次找到的较大元素交换位置。
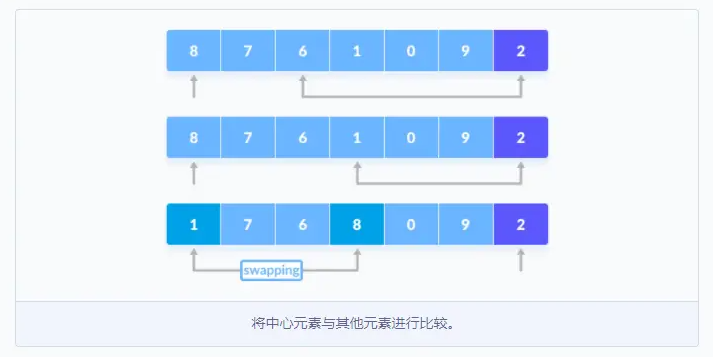
同样,重复该过程以将下一个更大的元素设置为第二指针,并且将其和另一个较小的元素交换位置。

该过程一直进行到到达倒数第二个元素为止。

最后将中心元素与第二个指针指向的元素交换位置。
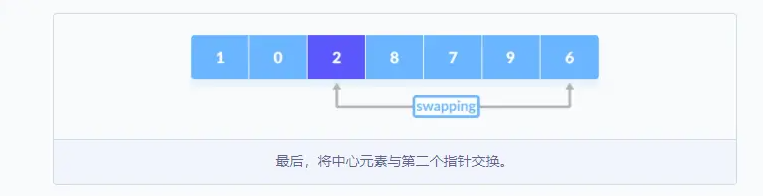
再次分别为左子部分和右子部分选择基准值,并且重复步骤2,子数组被分割,直到每个子数组只有一个元素,至此,该数组已经通过快速排序算法升序排好序了。
4.11.4算法分析
- 稳定性:不稳定
- 时间复杂度:最佳:O(nlogn), 最差:O(nlogn),平均:O(nlogn)
- 空间复杂度:O(logn)
4.11.5算法实现
import java.util.Arrays;
public class QuickSort {
public static void main(String[] args) {
int[] nums = {5, 2, 8, 3, 4, 7, 9, 10, 1, 6};
quickSort(nums, 0, nums.length - 1);
}
private static void quickSort(int[] nums, int start, int end) {
if (start < end) {
// 返回基准值
int partition = partition(nums, start, end);
// 左边序列递归进行快速排序
quickSort(nums, start, partition - 1);
// 右边序列递归进行快速排序
quickSort(nums, partition + 1, end);
}
}
public static int partition(int[] nums, int start, int end) {
// 1.首先将定义基准,这里以最后一个数做为基准
int pivot = nums[end];
// 2.定义指向比基准大的指针,首先指向第一个元素
int pointer = start;
// 3.遍历序列当中的每个元素
for (int i = start; i < end; i++) {
// 4.如果当前值小于基准值,则将当前值和最大的值交换位置。如果当前值大于基准值,则不交换
if (nums[i] <= pivot) {
int temp = nums[i];
nums[i] = nums[pointer];
nums[pointer] = temp;
// 5.最大值向前移动一个元素
pointer++;
}
System.out.println(Arrays.toString(nums));
}
// 6.一趟排序完成后,即此时元素已经遍历到基数的前一个数了,则交换基准值和当前下标为pointer的元素,该元素大于基准值。
// 使小于基准值的元素在左边,大于基准值的在右边
int temp = nums[pointer];
nums[pointer] = nums[end];
nums[end] = temp;
return pointer;
}
}输出结果和执行过程分析:
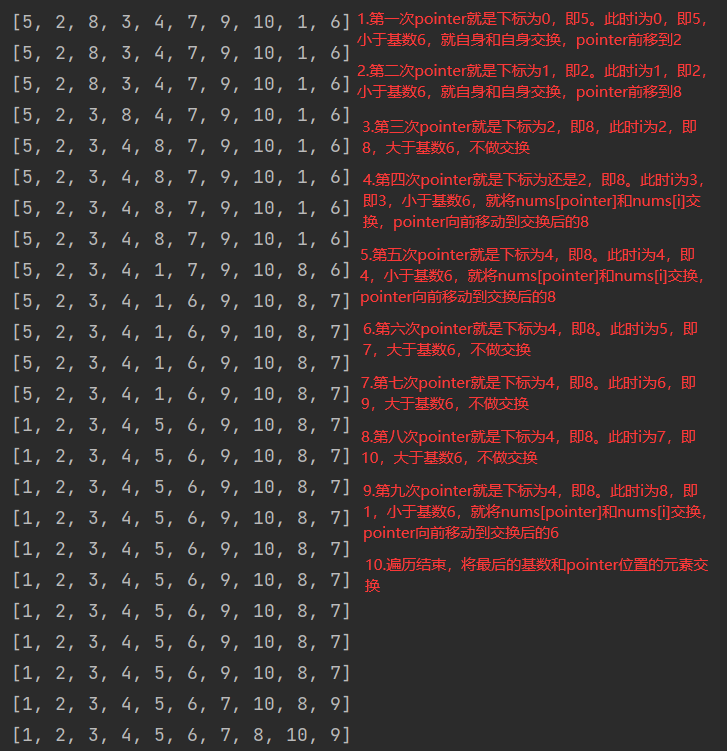
4.12基数排序(Radix sort)
4.12.1概述
- 基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort)或bin sort,顾名思义,它是通过键值的各个位的值,将要排序的元素分配至某些“桶”中,达到排序的作用。
- 基数排序法是属于稳定性的排序,基数排序法的是效率高的稳定性排序法。
- 基数排序(Radix Sort)是桶排序的扩展。
- 基数排序是1887年赫尔曼·何乐礼发明的。它是这样实现的:将整数按位数切割成不同的数字,然后按每个位数分别比较。
4.12.2算法步骤
首先定义10个“桶”,下标为0~9;然后遍历数组,按照元素的“个位”数值,依次放入对应下标的桶中,放完所有元素后,从第0个桶开始遍历,依次取出桶中元素按顺序放入原始数组中;同理,之后再遍历数组,按照元素的“十位”数值,做上一步相同的操作;以此类推,直到按照数组中最大元素的最高位操作完为止。
- 取得数组中的最大数,并取得位数,即为迭代次数
N(例如:数组中最大数值为 1000,则N=4);A为原始数组,从最低位开始取每个位组成radix数组;- 对
radix进行计数排序(利用计数排序适用于小范围数的特点);- 将
radix依次赋值给原数组;- 重复 2~4 步骤
N次
4.12.3图解算法

4.12.4算法分析
- 稳定性:稳定
- 时间复杂度:最佳:
O(n×k)最差:O(n×k)平均:O(n×k) - 空间复杂度:
O(n+k)
基数排序 vs 计数排序 vs 桶排序
这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:
- 基数排序:根据键值的每位数字来分配桶
- 计数排序:每个桶只存储单一键值
- 桶排序:每个桶存储一定范围的数值
4.12.5代码实现
- 首先判断该数组是否只有两位数,如果是直接返回,因为是直接排好序的
- 在数组中查找到最大元素,计算出其位数
- 创建一个List集合,List集合的泛型为<List
>,表示一个集合当中的桶数 - 根据位数遍历,将对应的位数的值的数放入到对应的桶当中
- 每遍历一次,就将集合当中的元素依次取出,并重新放入数组
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class RadixSort {
public static void main(String[] args) {
int[] nums = {5, 2, 8, 3, 4, 7, 9, 10, 1, 6};
int[] radixSort = radixSort(nums);
System.out.println(Arrays.toString(radixSort));
}
public static int[] radixSort(int[] nums) {
if (nums.length <= 2) {
return nums;
}
// 遍历数组,获取到最大的数
int max = nums[0];
for (int numbers : nums) {
if (numbers > max) {
max = numbers;
}
}
// 获取到循环的次数
int level = 1;
while (max / 10 != 0) {
level += 1;
max /= 10;
}
for (int i = 0; i < level; i++) {
List<List<Integer>> radix = new ArrayList<>();
// 初始化桶
for (int j = 0; j < 10; j++) {
radix.add(new ArrayList<>());
}
// 遍历每一个元素,根据level获取到当前每个元素当前位数的值,根据位数值添加到对应桶当中
for (int element : nums) {
// 获取到当前数对应位数上的值
int count = (element / (int) Math.pow(10, i)) % 10;
// 根据当前数对应位数上的值将当前元素添加到对应的桶当中
radix.get(count).add(element);
}
// 每一次循环结束,就遍历桶中的元素并重新添加到数组当中
int index = 0;
// 遍历每个桶
for (List<Integer> bucket : radix) {
// 遍历每个桶中的元素
for (Integer count : bucket) {
nums[index++] = count;
}
}
}
return nums;
}
}
5.线性查找、二分查找和插值查找
5.1线性查找
线性查找(Sequential Search)又叫顺序查找,是最基本的查找技术,它的查找过程是:从表中第一个(或最后一个)记录开始,逐个进行记录的关键字和给定值比较,若某个记录的关键字和给定值相等,则查找成功,找到所查的记录;如果直到最后一个(或第一个)记录,其关键字和给定值比较都不等时,则表中没有所查的记录,查找不成功。
5.2二分查找
5.2.1概述
二分查找(Binary Search)技术,又称为折半查找。它的前提是线性表中的记录必须是元素有序(通常从小到大有序),线性表必须采用顺序存储。它的查找过程是:在有序表中,取中间记录作为比较对象,若给定值与中间记录的关键字相等,则查找成功;若给定值小于中间记录的关键字,则在中间记录的左半区继续查找;若给定值大于中间记录的关键字,则在中间记录的右半区继续查找。不断重复上述过程,直到查找成功,或所有查找区域无记录,查找失败为止。
5.2.2基础二分查找
/**
* 二分查找基础
*
* @author Xu huaiang
* @date 2023/07/22
*/
public class BinarySearchBase {
public static int binarySearchBase(int[] arrays, int target) {
// 1.初始化指针
int start = 0, end = arrays.length - 1;
// 2.创建循环
while (start <= end) {
// 3.获取到中间索引
int middle = (start + end) / 2;
// 4.判断中间值和目标值大小
if (target < arrays[middle]) { //目标值在中间值左边,则末尾指针向左移动
end = middle - 1;
} else if (arrays[middle] < target) { //目标值在中间值右边,则起始指针向右移动
start = middle + 1;
} else {
return middle;
}
}
return -1;
}
}测试:
public class TestCentre {
public static void main(String[] args) {
int[] arrays1 = {1,2,3,4,5,6,7,8,9};
System.out.println(BinarySearchBase.binarySearchBase(arrays1,7));
}
}
打印出下标6。
5.2.3优化——避免数值溢出问题
在二分查找中,int middle = (start + end) >>> 1; 和 int middle = (start + end) / 2; 的区别在于前者使用了无符号右移运算符 >>>,而后者使用了除法运算符 /。
无符号右移运算符 >>> 会将 start + end 的二进制表示向右移动一位,相当于将其除以2。这种方法可以避免当 start + end 的值超过 int 类型的最大值时发生溢出的情况。因为它不会直接计算 start + end 的值,而是将 start + end 的二进制表示向右移动一位。这样,即使 start + end 的值超过了 int 类型的最大值,也不会发生溢出。
而后者直接使用除法运算符 / 进行除法运算,如果 start + end 的值超过 int 类型的最大值,就会发生溢出。
/**
* 二分查找 右移优化,避免超出类型所表示的最大整数
*
* @author Xu huaiang
* @date 2023/07/22
*/
public class BinarySearchUpdate {
public static int binarySearchBase(int[] arrays, int target) {
// 1.初始化指针
int start = 0, end = arrays.length - 1;
// 2.创建循环
while (start <= end) {
// 3.获取到中间索引,右移1位
int middle = (start + end) >>> 1;
// 4.判断中间值和目标值大小
if (target < arrays[middle]) { //目标值在中间值左边,则末尾指针向左移动
end = middle - 1;
} else if (arrays[middle] < target) { //目标值在中间值右边,则起始指针向右移动
start = middle + 1;
} else {
return middle;
}
}
return -1;
}
}5.2.4最左值匹配
- 当查找到元素时,不直接返回,而是将middle赋值给候选值,继续向左查找。当还存在arrays[middle] == target时,更新候选值,直到start > end结束
public class BinarySearchLeftMost {
public static int binarySearchBase(int[] arrays, int target) {
// 1.初始化指针
int start = 0, end = arrays.length - 1;
// 创建候选值
int candidate = -1;
// 2.创建循环
while (start <= end) {
// 3.获取到中间索引,右移1位
int middle = (start + end) >>> 1;
// 4.判断中间值和目标值大小
if (target < arrays[middle]) { //目标值在中间值左边,则末尾指针向左移动
end = middle - 1;
} else if (arrays[middle] < target) { //目标值在中间值右边,则起始指针向右移动
start = middle + 1;
} else {
// 相等时继续向左查找,直到start > end结束
candidate = middle;
end = middle - 1;
}
}
return candidate;
}
}5.2.5最右值匹配
- 当查找到元素时,不直接返回,而是将middle赋值给候选值,继续享有查找。当还存在arrays[middle] == target时,更新候选值,直到start > end结束
public class BinarySearchRightMost {
public static int binarySearchBase(int[] arrays, int target) {
// 1.初始化指针
int start = 0, end = arrays.length - 1;
int candidate = -1;
// 2.创建循环
while (start <= end) {
// 3.获取到中间索引,右移1位
int middle = (start + end) >>> 1;
// 4.判断中间值和目标值大小
if (target < arrays[middle]) { //目标值在中间值左边,则末尾指针向左移动
end = middle - 1;
} else if (arrays[middle] < target) { //目标值在中间值右边,则起始指针向右移动
start = middle + 1;
} else {
// 相等时继续向左查找,直到start > end结束
candidate = middle;
start = middle + 1;
}
}
return candidate;
}
}
5.3插值查找
5.3.1概述
插值查找算法类似于二分查找,也需要记录是有序的,不同的是插值查找每次从自适应mid处开始查找。
将二分查找求中间记录的mid 索引公式改成:

key:要查找的值;low:第一个记录在数组中的索引值;high:最后一个记录在数组中的索引值
(key-a[low]) / (a[high]-a[low])就是查找值在这个均匀分布的有序序列中的大致位置的系数
对应的代码公式为:
int mid = left + (right - left) * (value - arr[left]) / (arr[right] - arr[left]);5.3.2代码实现
public class InsertValueSearch {
public static int insertValueSearch(int[] nums, int left, int right, int target) {
if (left > right || target < nums[0] || target > nums[nums.length - 1]) {
return -1;
}
// 求出mid, 自适应
int middle = left + (right - left) * (target - nums[left]) / (nums[right] - nums[left]);
if (target < nums[middle]) {
return insertValueSearch(nums, middle + 1, right, target);
} else if (nums[middle] < target) {
return insertValueSearch(nums, middle - 1, right, target);
} else {
return middle;
}
}
}5.3.3注意事项
- 对于数据量较大,关键字分布比较均匀的查找表来说,采用插值查找, 速度较快
- 关键字分布不均匀的情况下,该方法不一定比折半查找要好
6.哈希表(散列表)
6.1概述
哈希表(Hash table,也叫散列表)是一种数据结构,它能够快速地存储和检索数据。哈希表通过使用一个散列函数将键映射到一个索引,然后在该索引处存储值。由于散列函数能够快速计算,因此哈希表能够在常数时间内完成插入和查找操作。
假设,我们为了方便记录某高校数学专业的所有学生的信息。要求可以按照学号(学号格式为:入学时间+年级+专业+专业内自增序号,如2011 1101 0001)能够快速找到某个学生的信息。这个时候我们可以取学号的自增序号部分,即后四位作为数组的索引下标,把学生相应的信息存储到对应的空间内即可。
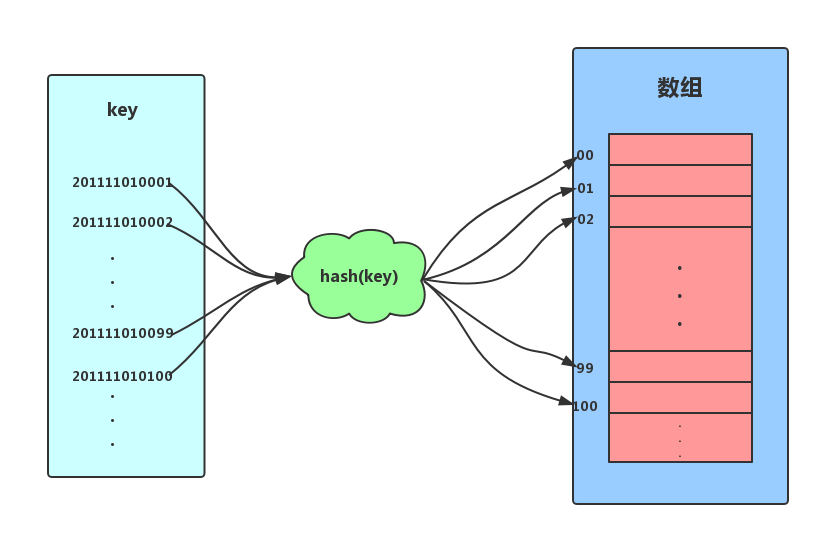
如上图所示,我们把学号作为key,通过截取学号后四位的函数后计算后得到索引下标,将数据存储到数组中。当我们按照键值(学号)查找时,只需要再次计算出索引下标,然后取出相应数据即可。以上便是散列思想。
6.2散列函数
6.2.1概述
上面的例子中,截取学号后四位的函数即是一个简单的散列函数。
Copy//散列函数 伪代码
int Hash(string key) {
// 获取后四位字符
string hashValue =int.parse(key.Substring(key.Length-4, 4));
// 将后两位字符转换为整数
return hashValue;
}在这里散列函数的作用就是将key值映射成数组的索引下标。关于散列函数的设计方法有很多,如:直接寻址法、数字分析法、随机数法等等。但即使是再优秀的设计方法也不能避免散列冲突。在散列表中散列函数不应设计太复杂。
好的散列函数满足两个原则:
- 计算简单
- 散列地址分布均匀
如果关键字是字符串如何处理?其实无论是英文字符,还是中文字符,也包括各种各样的符号,它们都可以转化为某种数字来对待,比如ASClI码或者Unicode码等,因此也就可以使用下面的这些方法。
总之,现实中,应该视不同的情况采用不同的散列函数。我们只能给出一些考虑的因素来提供参考:
- 计算散列地址所需的时间。
- 关键字的长度。
- 散列表的大小。
- 关键字的分布情况。
- 记录查找的频率。
综合这些因素,才能决策选择哪种散列函数更合适。
6.2.2直接定址法
取关键字或关键字的某个线性函数为Hash地址,即H(key)=key 或者H(key)=a*key+b,其中a和b为常数。
这样的散列函数优点就是简单、均匀,也不会产生冲突,但问题是这需要事先知道关键字的分布情况,适合查找表较小且连续的情况。由于这样的限制,在现实应用中,此方法虽然简单,但却并不常用。
6.2.3数字分析法
假设关键字是r进制数(如十进制数),并且Hash表中可能出现的关键字都是事先知道的,则可选取关键字的若干数位组成Hash地址。选取的原则是使得到的Hash地址尽量减少冲突,即所选数位上的数字尽可能是随机的。
若我们现在要存储某家公司员工登记表,如果用手机号作为关键字,那么极有可能前7位都是相同的。那么我们选择后面的四位成为散列地址就是不错的选择。如果这样的抽取工作还是容易出现冲突问题,还可以对抽取出来的数字再进行反转(如1234改成4321)、右环位移(如1234改成4123)、左环位移、甚至前两数与后两数叠加(如1234改成12+34=46)等方法。总的目的就是为了提供一个散列函数,能够合理地将关键字分配到散列表的各位置。
数字分析法通常适合处理关键字位数比较大的情况,如果事先知道关键字的分布且关键字的若干位分布较均匀,就可以考虑用这个方法。
6.2.4平方取中法
取关键字平方后的中间几位作为Hash地址。通常在选定Hash函数的时候不一定能知道关键字的全部情况,仅取其中的几位为地址不一定合适,而一个数平方后的中间几位数和数的每一位都相关,由此得到的Hash地址随机性更大,取的位数由表长决定。
平方取中法比较适合于不知道关键字的分布,而位数又不是很大的情况。
6.2.5折叠法
折叠法是将关键字从左到右分割成位数相等的几部分,然后将这几部分叠加求和,并按散列表表长,取后几位作为散列值。
比如我们的关键字是9876543210,散列表表长为三位,我们将它分为四组,
987|654|321|0,然后将它们叠加求和987+654+321+0=1962,再求后3位得到散列地址为962。
有时可能这还不能够保证分布均匀,不妨从一端向另一端来回折叠后对齐相加。
比如我们将987和321反转,再与654和0相加,变成789+654+123+0=1566,此时散列地址为566。
6.2.6除留余数法(常用)
取关键字被某个不大于Hash表表长m的数p除后所得的余数为Hash地址,即
H(key)=key mod p(p≤m)
在本方法中,p的选择很重要,一般p选择小于或者等于表长的最大素数,这样可以减少冲突。
6.2.7随机数法
选择一个随机数,取关键字的随机函数值为它的散列地址。也就是f(key)= random(key)。这里random是随机函数。当关键字的长度不等时,采用这个方法构造散列函数是比较合适的。
6.3哈希冲突
6.3.1概念
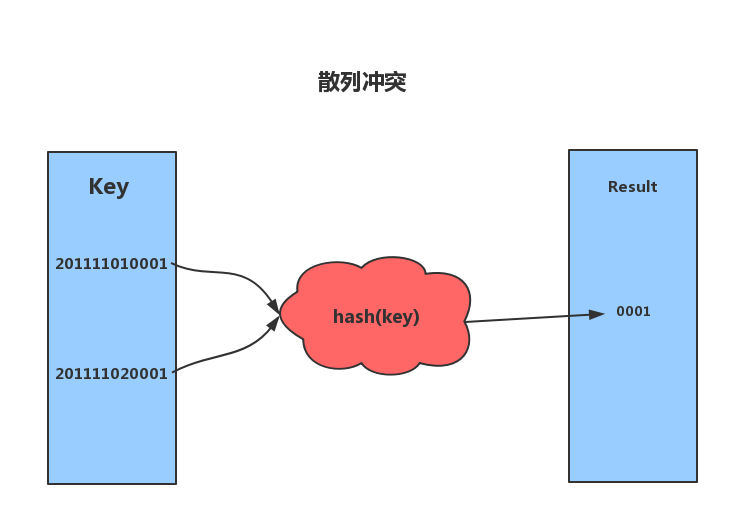
哈希冲突(Hash Collision)指的是当两个不同的输入在经过哈希算法处理后产生了相同的散列值。由于散列值的长度是固定的,而输入的长度是不确定的,所以理论上总会存在哈希冲突的可能性。为了解决哈希冲突问题,常用的方法有开放寻址法和链地址法。
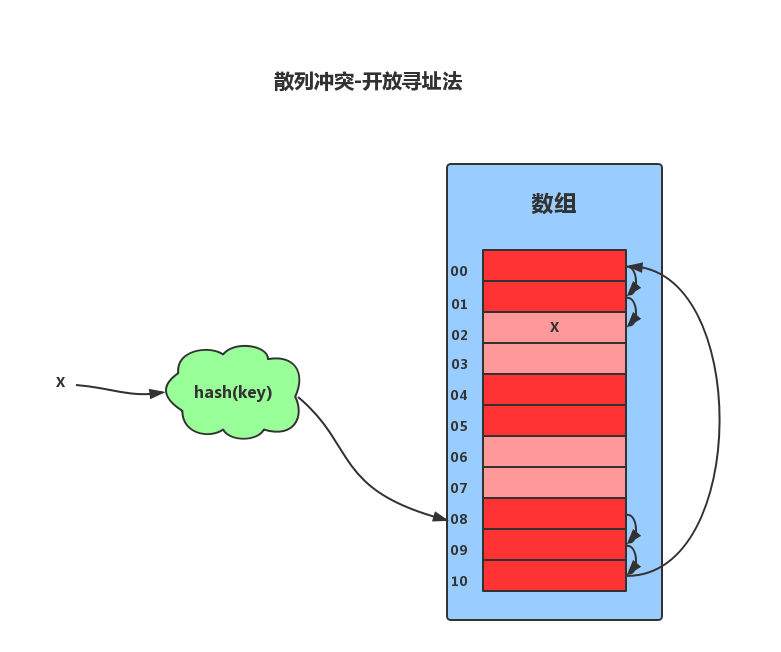
6.3.2开放寻址法
开放寻址法的核心思想是,如果出现了散列冲突,我们就重新探测一个空闲位置,将其插入。比如,我们可以使用线性探测法。当我们往散列表中插入数据时,如果某个数据经过散列函数散列之后,存储位置已经被占用了,我们就从当前位置开始,依次往后查找,看是否有空闲位置,如果遍历到尾部都没有找到空闲的位置,那么我们就再从表头开始找,直到找到为止。
散列表中查找元素的时候,我们通过散列函数求出要查找元素的键值对应的散列值,然后比较数组中下标为散列值的元素和要查找的元素。如果相等,则说明就是我们要找的元素;否则就顺序往后依次查找。如果遍历到数组中的空闲位置还没有找到,就说明要查找的元素并没有在散列表中。
对于删除操作稍微有些特别,不能单纯地把要删除的元素设置为空。因为在查找的时候,一旦我们通过线性探测方法,找到一个空闲位置,我们就可以认定散列表中不存在这个数据。但是,如果这个空闲位置是我们后来删除的,就会导致原来的查找算法失效。这里我们可以将删除的元素,特殊标记为 deleted。当线性探测查找的时候,遇到标记为 deleted 的空间,并不是停下来,而是继续往下探测。
线性探测法存在很大问题。当散列表中插入的数据越来越多时,其散列冲突的可能性就越大,极端情况下甚至要探测整个散列表,因此最坏时间复杂度为O(N)。在开放寻址法中,除了线性探测法,我们还可以二次探测和双重散列等方式。
6.3.3链表法
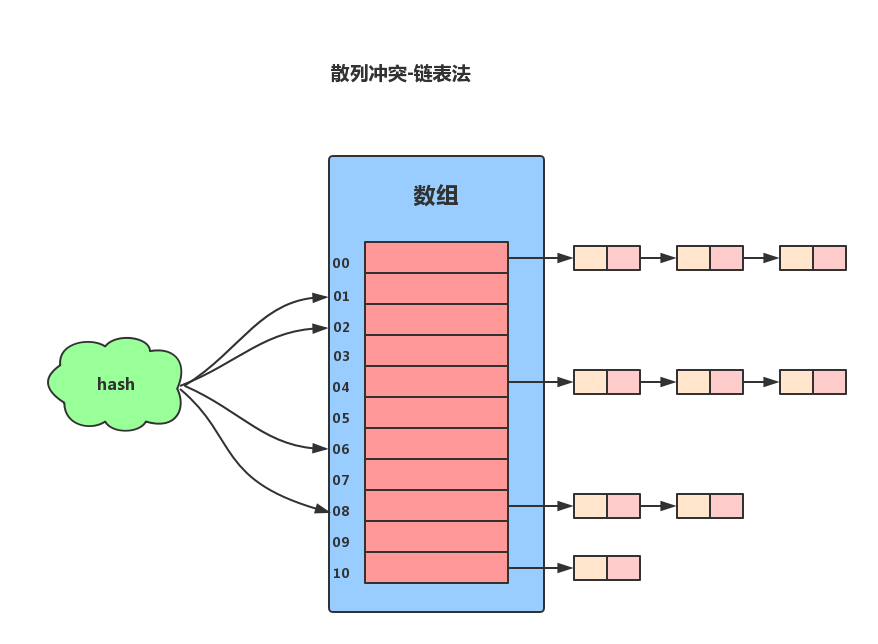
简单来讲就是在冲突的位置插入一条链表来存储数据。
链表法是一种比较常用的散列冲突解决办法,Redis使用的就是链表法来解决散列冲突。链表法的原理是:如果遇到冲突,他就会在原地址新建一个空间,然后以链表结点的形式插入到该空间。当插入的时候,我们只需要通过散列函数计算出对应的散列槽位,将其插入到对应链表中即可。
6.3.4开放寻址法与链表法比较
对于开放寻址法解决冲突的散列表,由于数据都存储在数组中,因此可以有效地利用 CPU 缓存加快查询速度(数组占用一块连续的空间)。但是删除数据的时候比较麻烦,需要特殊标记已经删除掉的数据。而且,在开放寻址法中,所有的数据都存储在一个数组中,比起链表法来说,冲突的代价更高。所以,使用开放寻址法解决冲突的散列表,负载因子的上限不能太大。这也导致这种方法比链表法更浪费内存空间。
对于链表法解决冲突的散列表,对内存的利用率比开放寻址法要高。因为链表结点可以在需要的时候再创建,并不需要像开放寻址法那样事先申请好。链表法比起开放寻址法,对大装载因子的容忍度更高。开放寻址法只能适用装载因子小于1的情况。接近1时,就可能会有大量的散列冲突,性能会下降很多。但是对于链表法来说,只要散列函数的值随机均匀,即便装载因子变成10,也就是链表的长度变长了而已,虽然查找效率有所下降,但是比起顺序查找还是快很多。但是,链表因为要存储指针,所以对于比较小的对象的存储,是比较消耗内存的,而且链表中的结点是零散分布在内存中的,不是连续的,所以对CPU缓存是不友好的,这对于执行效率有一定的影响。
6.4哈希表实现
下面是一个简单的哈希表实现。它使用了数组和链表来实现哈希表。哈希表中的每个元素都是一个链表,链表中存储了具有相同散列值的元素。
HashTable类中定义了一个add方法,用于向哈希表中添加元素。它首先通过散列函数计算出元素的散列值,然后将元素添加到对应的链表中。
hashFunction方法是一个简单的散列函数,它将输入数据 id 除以 size 取余数作为散列值。
list方法用于遍历哈希表中的所有链表。
getEmp方法用于在哈希表中查找指定id的元素。它首先通过散列函数计算出元素所在链表的索引,然后在该链表中查找指定id的元素。
Emp类表示员工,包含员工的id和姓名。
EmpLinkedList类表示链表结构,包含一个头指针和一些方法,如添加元素、遍历元素和查找元素等。
public class HashTableDemo {
public static void main(String[] args) {
HashTable hashTable = new HashTable(7);
hashTable.add(new Emp(1,"张三"));
hashTable.add(new Emp(2,"李四"));
hashTable.add(new Emp(8,"王五"));
hashTable.list();
Emp emp = hashTable.getEmp(1);
if (emp != null){
System.out.println("查找的Emp信息:" + emp);
} else {
System.out.println("未找到当前Emp!");
}
}
}
/**
* 哈希表(数组 + 链表)
*
* @author Xu huaiang
* @date 2023/07/31
*/
class HashTable {
private EmpLinkedList[] empLinkedList;
private int size;
public HashTable(int size) {
this.size = size;
this.empLinkedList = new EmpLinkedList[size];
// 数组元素初始化
for (int i = 0; i < size; i++) {
empLinkedList[i] = new EmpLinkedList();
}
}
/**
* 根据数据id,将数据添加到对应的链表中
*
* @param emp 员工
*/
public void add(Emp emp) {
// 获取到散列值
int empLinkedListNO = hashFunction(emp.id);
// 将元素添加到对应的链表中
empLinkedList[empLinkedListNO].add(emp);
}
/**
* 定义一个简单的散列函数。它将输入数据 id 除以 size 取余数作为散列值
*
* @param id id
* @return int
*/
public int hashFunction(int id) {
return id % size;
}
/**
* 遍历数组中的所有链表(遍历哈希表)
*/
public void list(){
for (int i = 0; i < size; i++) {
empLinkedList[i].list(i);
}
}
public Emp getEmp(int id){
int empLinkedListNO = hashFunction(id);
Emp emp = empLinkedList[empLinkedListNO].getEmp(id);
return emp;
}
}
/**
* Emp类
*
* @author Xu huaiang
* @date 2023/07/31
*/
class Emp {
public int id;
public String name;
public Emp next;
public Emp(int id, String name) {
super();
this.id = id;
this.name = name;
}
@Override
public String toString() {
return "Emp{" +
"id=" + id +
", name='" + name + '\'' +
'}';
}
}
/**
* 链表结构
*
* @author Xu huaiang
* @date 2023/07/31
*/
class EmpLinkedList {
// 头指针
private Emp head;
/**
* 链表添加元素
*
* @param emp 电磁脉冲
*/
public void add(Emp emp) {
// 如果是第一个元素
if (head == null) {
head = emp;
return;
}
Emp currentEmp = head;
while (currentEmp.next != null) {
currentEmp = currentEmp.next;
}
// 添加新元素
currentEmp.next = emp;
}
/**
* 遍历元素
*/
public void list(int no) {
if (head == null) {
System.out.println("当前" + (no + 1) +"链表为空!");
return;
}
System.out.print("当前" + (no + 1) +"链表信息为:");
Emp currentEmp = head;
while (currentEmp != null) {
System.out.print(currentEmp + "->");
currentEmp = currentEmp.next;
}
System.out.println();
}
public Emp getEmp(int id){
if (head == null){
System.out.println("链表为空!");
return null;
}
Emp currentEmp = head;
while (currentEmp != null){
if (currentEmp.id == id){
break;
}
// 遍历当前链表未找到
if (currentEmp == null){
break;
}
// 后移
currentEmp = currentEmp.next;
}
return currentEmp;
}
}
7.树
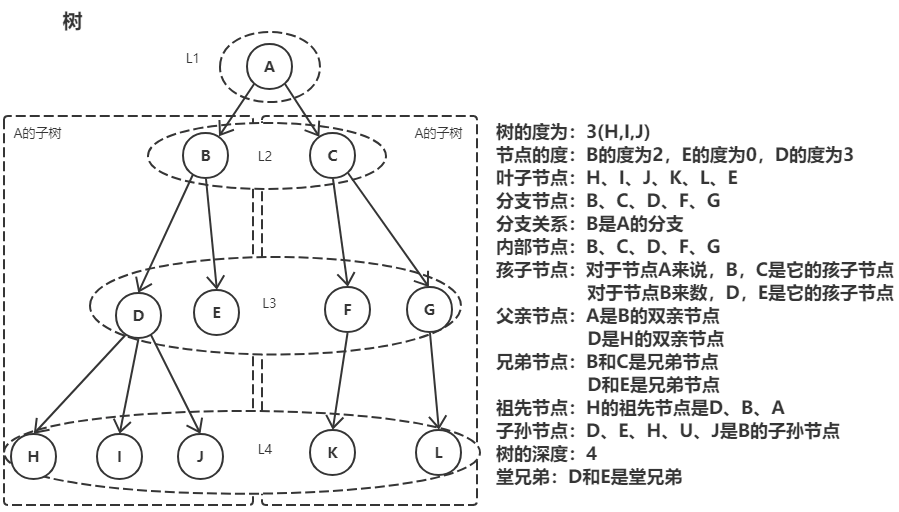
7.1树的概念
树(Tree)是n(n>=0)个结点的有限集。n=0时称为空树。
在任意一颗非空树中:
- 有且仅有一个特定的称为根(Root)的结点。
- 当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1、T2、…..、Tm,其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)
7.2树的常用术语
| 名称 | 含义 |
|---|---|
| 节点 | 树中的数据元素 |
| 树的度 | 树内各节点的度的最大值 |
| 节点的度 | 节点拥有的子树的数目称为度,记作d(v) |
| 叶子节点 | 节点的度数为0,称为叶子节点leaf、终端节点、末端节点 |
| 分支节点 | 节点度数不为0,称为非终端节点或分支节点 |
| 分支 | 节点之间的关系 |
| 内部节点 | 除根节点外的分支节点,当然也不包括叶子节点 |
| 孩子节点 | 节点的子树的根节点成为该节点的孩子 |
| 双亲节点 | 父节点,即该节点的前驱 |
| 兄弟节点 | 具有相同双亲节点的节点 |
| 祖先节点 | 从根节点到该节点所经分支上所有的节点。 |
| 子孙节点 | 节点的所有子树上的节点都成为该节点的子孙。 |
| 节点的层次 | 根节点为第一层,根的孩子为第二层,依次类推记作(Lv) |
| 树的深度 | 节点的层次的最大值 |
| 堂兄弟 | 双亲在同一层的节点 |
| 有序树 | 结点的子树是有顺序的(兄弟有大小,有先后次序),不能交换 |
| 无序数 | 结点的子树是无序的,可以交换 |
| 路径 | 树中的k个节点n1、n2、…nk,满足ni是n(i+1)的双亲,成为n1到nk的一条路径。就是一条线串下来的,前一个都是后一个父(前驱)节点。 |
| 森林 | m(m≥0)课不相交的树的集合,对于节点而言,其子树的集合就是森林。 |
二叉树(Binary Tree)是n(n>=0)个节点的有限集合,该集合可以为空集(称为空二叉树),或者由一个根节点和两个互不相交的、分别称为根节点的左子树和右子树的二叉树组成。
7.3二叉树
每个节点最多只能有两个子节点的树叫做二叉树。二叉树的子节点分为左节点和右节点。
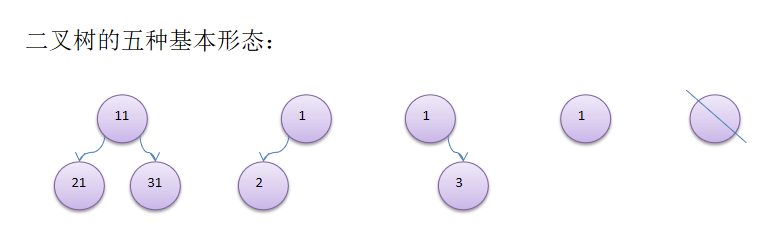
7.3.1二叉树的5种基本形态
- 根节点既有左子树,又有右子树
- 根节点只有左子树
- 根节点只有右子树
- 只有一个根节点
- 空二叉树
7.3.2二叉树特点
- 每个节点最多有两个子树,所以二叉树不存在度大于2的节点,可以没有子树或者一个子树。
- 左子树和右子树有顺序,次序不能任意颠倒。
- 即使树中某节点只有一颗子树,也要区分是左子树还是右子树。
7.3.3特殊二叉树
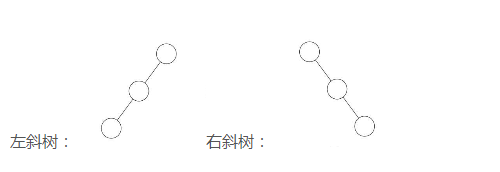
斜树:所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树。
斜树有很明显的特点,就是每一层都只有一个结点,结点的个数与二叉树的深度相同。线性表结构就可以理解为是树的一种极其特殊的表现形式。
满二叉树:在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。
满二叉树的特点有:
- 叶子只能出现在最下一层。
- 非叶子结点的度一定是2。
- 在同样深度的二叉树中,满二叉树的结点个数最多,叶子数最多。
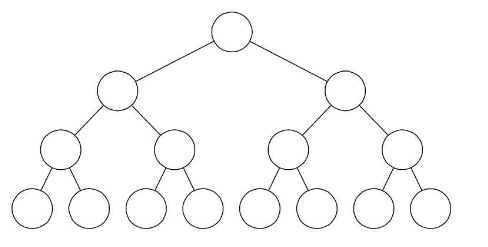
完全二叉树:对一棵具有n个结点的二叉树按层序编号,如果编号为i(1<i<n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树。
满二叉树一定是一棵完全二叉树,但完全二叉树不一定是满的。
完全二叉树的特点:
- 叶子结点只能出现在最下两层。
- 最下层的叶子一定集中在左部连续位置。
- 倒数二层,若有叶子结点,一定都在右部连续位置。
- 如果结点度为1,则该结点只有左孩子,即不存在只有右子树的情况。
- 同样结点数的二叉树,完全二又树的深度最小。
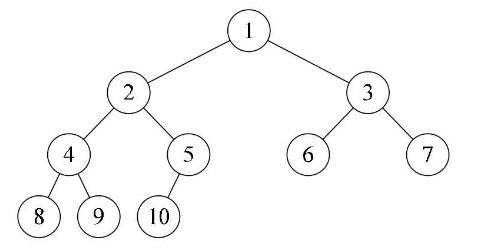
7.3.4二叉树性质
- 在二叉树的第i层上至多有2i-1个结点(i>=1)
- 深度为k的二叉树至多有2k-1个结点(k>=1)
- 对任何一棵二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0 = n2+1。
- 具有n个结点的完全二叉树的深度为[log2n ] + 1 ([X]表示不大于X的最大整数)。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到第[log2n ] + 1层,每层从左到右),对任一结点 i (1<=i<=n)有:
- 如果 i=1,则结点i是二叉树的根,无双亲;如果 i>1,则其双亲是结点[i/2]。
- 如果 2i>n,则结点i无左孩子(结点i为叶子结点);否则其左孩子是结点2i。
- 如果 2i+1>n,则结点i无右孩子;否则其右孩子是结点2i+1。
结合下图理解:

7.3.5二叉树的遍历
二叉树的遍历是指从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且仅被访问一次。
7.3.5.1前中后序遍历的介绍
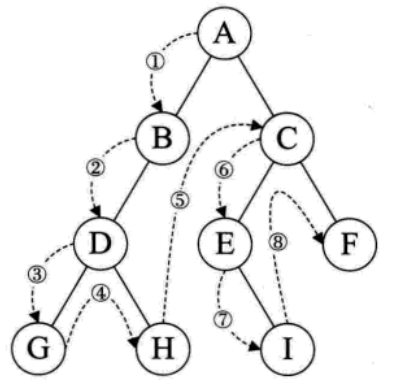
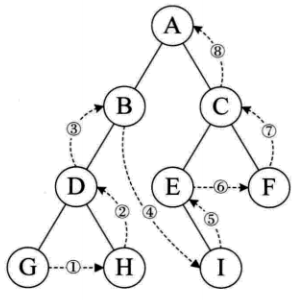
前序遍历(根节点->左子树->右子树):规则是若二叉树为空,则空操作返回,否则先访问根结点,然后前序遍历左子树,再前序遍历右子树。如图所示,遍历的顺序为:ABDGHCEIF。
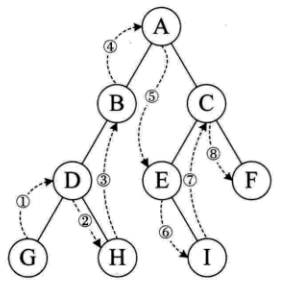
中序遍历(左子树->根节点->右子树):规则是若树为空,则空操作返回,否则从根结点开始(注意并不是先访问根结点),中序遍历根结点的左子树,然后是访问根结点,最后中序遍历右子树。如图所示,遍历的顺序为:GDHBAEICF。
后序遍历(左子树->右子树->根节点):规则是若树为空,则空操作返回,否则从左到右的方式遍历访问左右子树,最后访问根结点**。如图所示,遍历的顺序为:GHDBIEFCA。
7.3.5.2前中后序遍历的代码实现
package com.nanzx.tree;
public class BinaryTreeDemo {
public static void main(String[] args) {
// 先创建一颗二叉树
BinaryTree binaryTree = new BinaryTree();
// 创建需要的结点
HeroNode root = new HeroNode(1, "宋江");
HeroNode node2 = new HeroNode(2, "吴用");
HeroNode node3 = new HeroNode(3, "卢俊义");
HeroNode node4 = new HeroNode(4, "林冲");
HeroNode node5 = new HeroNode(5, "关胜");
// 先手动创建该二叉树,后面学习递归的方式创建二叉树
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root);
// 测试
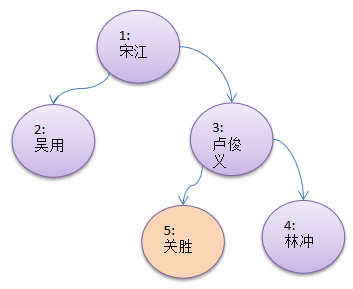
System.out.println("前序遍历"); // 1,2,3,5,4
binaryTree.preOrder();
System.out.println("中序遍历");
binaryTree.infixOrder(); // 2,1,5,3,4
System.out.println("后序遍历");
binaryTree.postOrder(); // 2,5,4,3,1
}
}
class BinaryTree {
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
// 前序遍历
public void preOrder() {
if (this.root != null) {
this.root.preOrder();
} else {
System.out.println("二叉树为空,无法遍历");
}
}
// 中序遍历
public void infixOrder() {
if (this.root != null) {
this.root.infixOrder();
} else {
System.out.println("二叉树为空,无法遍历");
}
}
// 后序遍历
public void postOrder() {
if (this.root != null) {
this.root.postOrder();
} else {
System.out.println("二叉树为空,无法遍历");
}
}
}
class HeroNode {
private int no;
private String name;
private HeroNode left;
private HeroNode right;
public HeroNode(int no, String name) {
super();
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
}
// 前序遍历
public void preOrder() {
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
// 中序遍历
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.infixOrder();
}
}
// 后序遍历
public void postOrder() {
if (this.left != null) {
this.left.postOrder();
}
if (this.right != null) {
this.right.postOrder();
}
System.out.println(this);
}
}7.3.5.3前中后序查找的代码实现
- 前序查找思路
- 先判断当前结点的no是否等于要查找的
- 如果是相等,则返回当前结点
- 如果不等,则判断当前结点的左子节点是否为空,如果不为空,则递归前序查找
- 如果左递归前序查找,找到结点,则返回,否继续判断,当前的结点的右子节点是否为空,如果不空,则继续向右递归前序查找
- 中序查找思路
- 判断当前结点的左子节点是否为空,如果不为空,则递归中序查找
- 如果找到,则返回,如果没有找到,就和当前结点比较,如果是则返回当前结点,否则继续进行右递归的中序查找
- 如果右递归中序查找,找到就返回,否则返回null
- 后序查找思路
- 判断当前结点的左子节点是否为空,如果不为空,则递归后序查找
- 如果找到,就返回,如果没有找到,就判断当前结点的右子节点是否为空,如果不为空,则右递归进行后序查找,如果找到,就返回
- 就和当前结点进行,比如,如果是则返回,否则返回null
package com.nanzx.tree;
public class BinaryTreeDemo {
public static void main(String[] args) {
// 先创建一颗二叉树
BinaryTree binaryTree = new BinaryTree();
// 创建需要的结点
HeroNode root = new HeroNode(1, "宋江");
HeroNode node2 = new HeroNode(2, "吴用");
HeroNode node3 = new HeroNode(3, "卢俊义");
HeroNode node4 = new HeroNode(4, "林冲");
HeroNode node5 = new HeroNode(5, "关胜");
// 先手动创建该二叉树,后面学习递归的方式创建二叉树
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root);
//前序遍历查找的次数 4次
System.out.println("前序遍历方式~~~");
HeroNode resNode = binaryTree.preOrderSearch(5);
if (resNode != null) {
System.out.printf("找到了,信息为 no=%d name=%s", resNode.getNo(), resNode.getName());
} else {
System.out.printf("没有找到 no = %d 的英雄", 5);
}
//中序遍历查找的次数 3次
// System.out.println("中序遍历方式~~~");
// HeroNode resNode = binaryTree.infixOrderSearch(5);
// if (resNode != null) {
// System.out.printf("找到了,信息为 no=%d name=%s", resNode.getNo(), resNode.getName());
// } else {
// System.out.printf("没有找到 no = %d 的英雄", 5);
// }
//后序遍历查找的次数 2次
// System.out.println("后序遍历方式~~~");
// HeroNode resNode = binaryTree.postOrderSearch(5);
// if (resNode != null) {
// System.out.printf("找到了,信息为 no=%d name=%s", resNode.getNo(), resNode.getName());
// } else {
// System.out.printf("没有找到 no = %d 的英雄", 5);
// }
}
}
class BinaryTree {
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
// 前序遍历查找
public HeroNode preOrderSearch(int no) {
if (root != null) {
return root.preOrderSearch(no);
} else {
return null;
}
}
// 中序遍历查找
public HeroNode infixOrderSearch(int no) {
if (root != null) {
return root.infixOrderSearch(no);
} else {
return null;
}
}
// 后序遍历查找
public HeroNode postOrderSearch(int no) {
if (root != null) {
return this.root.postOrderSearch(no);
} else {
return null;
}
}
}
class HeroNode {
private int no;
private String name;
private HeroNode left;
private HeroNode right;
public HeroNode(int no, String name) {
super();
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
}
// 前序遍历查找
public HeroNode preOrderSearch(int no) {
System.out.println("进入前序遍历");
// 比较当前结点是不是
if (this.no == no) {
return this;
}
// 1.判断当前结点的左子节点是否为空,如果不为空,则递归前序查找
// 2.如果左递归前序查找,找到结点,则返回
HeroNode resNode = null;
if (this.left != null) {
resNode = this.left.preOrderSearch(no);
}
if (resNode != null) {// 说明我们左子树找到
return resNode;
}
// 1.左递归前序查找,找到结点,则返回,否继续判断,
// 2.当前的结点的右子节点是否为空,如果不空,则继续向右递归前序查找
if (this.right != null) {
resNode = this.right.preOrderSearch(no);
}
return resNode;
}
// 中序遍历查找
public HeroNode infixOrderSearch(int no) {
HeroNode resNode = null;
if (this.left != null) {
resNode = this.left.infixOrderSearch(no);
}
if (resNode != null) {
return resNode;
}
System.out.println("进入中序查找");
if (this.no == no) {
return this;
}
if (this.right != null) {
resNode = this.right.infixOrderSearch(no);
}
return resNode;
}
// 后序遍历查找
public HeroNode postOrderSearch(int no) {
HeroNode resNode = null;
if (this.left != null) {
resNode = this.left.postOrderSearch(no);
}
if (resNode != null) {
return resNode;
}
if (this.right != null) {
resNode = this.right.postOrderSearch(no);
}
if (resNode != null) {
return resNode;
}
System.out.println("进入后序查找");
if (this.no == no) {
return this;
}
return resNode;
}
}7.2.5.4删除节点的代码实现
- 因为我们的二叉树是单向的,所以我们是判断当前结点的子结点是否需要删除结点,而不能去判断当前这个结点是不是需要删除结点
- 如果当前结点的左子结点不为空,并且左子结点就是要删除结点,就将this.left=null;并且就返回(结束递归删除)
- 如果当前结点的右子结点不为空,并且右子结点就是要删除结点,就将this.right=null ;并且就返回(结束递归删除)
- 如果第2和第3步没有删除结点,那么我们就需要向左子树进行递归删除
- 如果第4步也没有删除结点,则应当向右子树进行递归删除.
- 考虑如果树是空树root,如果只有一个root结点,则等价将二叉树置空
package com.nanzx.tree;
public class BinaryTreeDemo {
public static void main(String[] args) {
// 先创建一颗二叉树
BinaryTree binaryTree = new BinaryTree();
// 创建需要的结点
HeroNode root = new HeroNode(1, "宋江");
HeroNode node2 = new HeroNode(2, "吴用");
HeroNode node3 = new HeroNode(3, "卢俊义");
HeroNode node4 = new HeroNode(4, "林冲");
HeroNode node5 = new HeroNode(5, "关胜");
// 先手动创建该二叉树,后面学习递归的方式创建二叉树
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root);
// 测试一把删除结点
System.out.println("删除前,前序遍历");
binaryTree.preOrder(); // 1,2,3,5,4
binaryTree.delNode(5);
System.out.println("删除后,前序遍历");
binaryTree.preOrder(); // 1,2,3,4
}
}
class BinaryTree {
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
// 删除结点
public void delNode(int no) {
if (root != null) {
// 如果只有一个root结点, 这里立即判断root是不是就是要删除结点
if (root.getNo() == no) {
root = null;
} else {
// 递归删除
root.delNode(no);
}
} else {
System.out.println("空树,不能删除~");
}
}
// 前序遍历
public void preOrder() {
if (this.root != null) {
this.root.preOrder();
} else {
System.out.println("二叉树为空,无法遍历");
}
}
}
class HeroNode {
private int no;
private String name;
private HeroNode left;
private HeroNode right;
public HeroNode(int no, String name) {
super();
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
}
// 递归删除结点
// 1.如果删除的节点是叶子节点,则删除该节点
// 2.如果删除的节点是非叶子节点,则删除该子树
public void delNode(int no) {
// 1.因为我们的二叉树是单向的,所以我们是判断当前结点的子结点是否需要删除结点,而不能去判断当前这个结点是不是需要删除结点.
// 2.如果当前结点的左子结点不为空,并且左子结点就是要删除结点,就将this.left = null; 并且就返回(结束递归删除)
if (this.left != null && this.left.no == no) {
this.left = null;
return;
}
// 3.如果当前结点的右子结点不为空,并且右子结点就是要删除结点,就将this.right= null ;并且就返回(结束递归删除)
if (this.right != null && this.right.no == no) {
this.right = null;
return;
}
// 4.我们就需要向左子树进行递归删除
if (this.left != null) {
this.left.delNode(no);
}
// 5.则应当向右子树进行递归删除
if (this.right != null) {
this.right.delNode(no);
}
}
// 前序遍历
public void preOrder() {
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
}7.4二叉排序树(BST树)
7.4.1基本介绍
二叉排序树(Binary Sort Tree),又称为二叉搜索树。它或者是一棵空树,或者是具有下列性质的二叉树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树。
- 特别说明:如果有相同的值,可以将该节点放在左子节点或右子节点
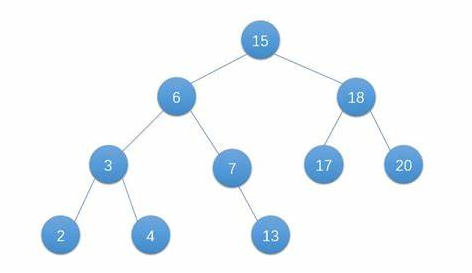
7.4.2二叉树构建代码实现
package com.nanzx.binarysorttree;
public class BinarySortTreeDemo {
public static void main(String[] args) {
int[] arr = { 7, 3, 10, 12, 5, 1, 9};
BinarySortTree binarySortTree = new BinarySortTree();
// 循环的添加结点到二叉排序树
for (int i = 0; i < arr.length; i++) {
binarySortTree.add(new Node(arr[i]));
}
// 中序遍历二叉排序树
System.out.println("中序遍历二叉排序树~");
binarySortTree.infixOrder(); // 1, 3, 5, 7, 9, 10, 12
}
}
class BinarySortTree {
private Node root;
public Node getRoot() {
return root;
}
// 添加结点的方法
public void add(Node node) {
if (root == null) {
root = node;
} else {
root.add(node);
}
}
// 中序遍历
public void infixOrder() {
if (root != null) {
root.infixOrder();
} else {
System.out.println("二叉排序树为空,不能遍历");
}
}
}
class Node {
int value;
Node left;
Node right;
public Node(int value) {
super();
this.value = value;
}
@Override
public String toString() {
return "Node [value=" + value + "]";
}
public void add(Node node) {
if (node == null) {
return;
}
//判断当前传入的值和当前子树的根节点的关系
if (node.value < this.value) {
//如果根节点的左节点为空,则直接添加到左节点
if (this.left == null) {
this.left = node;
} else {
//递归向左子树添加
this.left.add(node);
}
} else {
//如果根节点的右节点为空,则直接添加到右节点
if (this.right == null) {
this.right = node;
} else {
//递归向右子树添加
this.right.add(node);
}
}
}
//中序遍历
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this.value);
if (this.right != null) {
this.right.infixOrder();
}
}
}7.5平衡二叉树(AVL树、平衡二叉搜索树)
7.5.1平衡二叉树为什么会出现
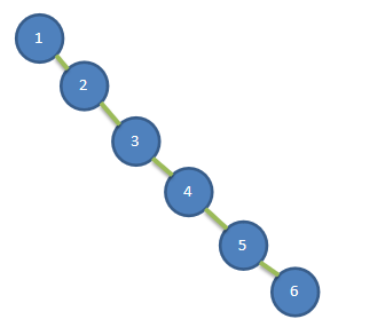
二叉搜索树(BST)存在的问题是:树在插入的时候会导致倾斜,不同的插入顺序会导致树的高度不一样,而树的高度直接影响了树的查找效率。最坏的情况所有的节点都在一条斜线上,这样树的高度为N,这样就变成了一个链表。基于BST存在的问题,平衡查找二叉树(Balanced BST)产生了。
平衡树的插入和删除的时候,会通过旋转操作将高度保持在LogN。
7.5.2概念
平衡二叉树:也叫平衡二叉搜索树(Self-balancing binary search tree),又被称为AVL树, 可以保证查询效率较高。
特点:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。
一棵AVL树有如下必要条件:
- 条件一:它必须是二叉排序树。
- 条件二:每个节点的左子树和右子树的高度差至多为1。即平衡二叉树要求平衡因子的绝对值不大于1
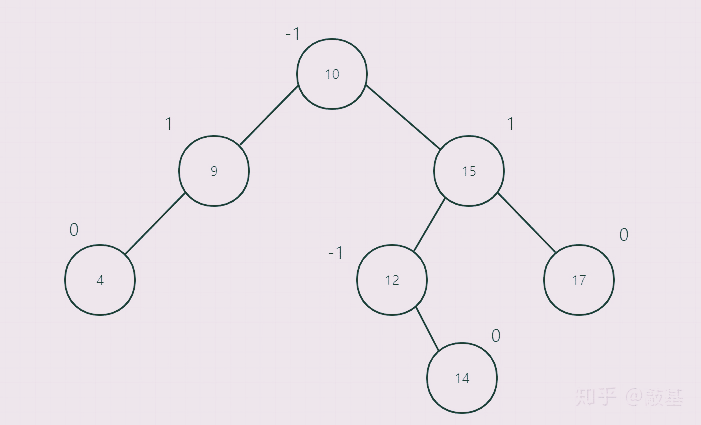
7.5.3不平衡与左旋转、右旋转
7.5.3.1不平衡
不平衡即出现了绝对值大于1的平衡因子。
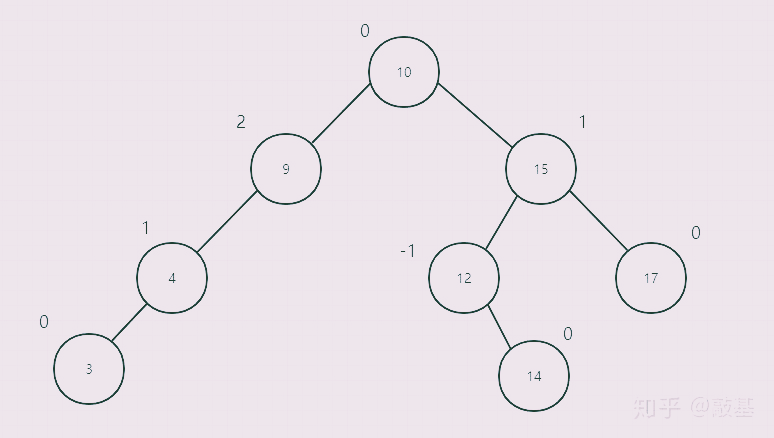
插入3之后,9的平衡因子变为2。二叉树失去平衡,需要通过旋转来重新平衡。
7.5.3.2旋转类型的判定
离插入点最近的,平衡因子的绝对值大于1的点称为失衡点。
从失衡点开始,沿树“寻找”插入点。且只记录“寻找”的前两步的路径方向。由此判定旋转类型。
- LL旋转(右旋)
以上图为例。插入点为3,失衡点为9。从9开始,“寻找”3。发现3在9的左子树的左子树上。将路径简记为“左左”。所以需要LL旋转。
- LR旋转(先左后右双旋)
从失衡点5开始,“寻找”插入点4。将路径简记为“左右”。所以需要LR旋转。
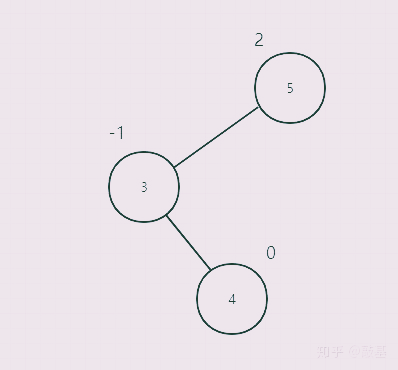
- RR旋转(左旋)
寻找”路径简记为“右右”。所以需要RR旋转。
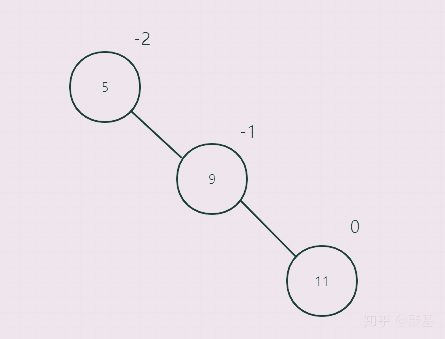
- RL旋转(先右后左双旋)
“寻找”路径简记为“右左”。所以需要RL旋转。
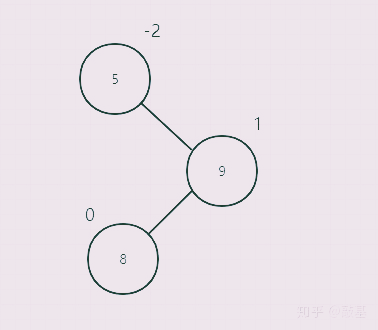
7.5.4二叉平衡树的构建过程
旋转方法:
方法与旋转类型无关。且一种方法就可应对四种旋转类型。
从失衡点开始,向插入点寻找,经过两步“寻找”,则必然遇到两个结点。加上失衡点,总共三个结点。假设为A、B、C,并规定A<B<C。将这三个结点单独拿出来。把其中的“中位数”B作为根结点,A作为B的左子树,C作为B的右子树,构建一个新的平衡二叉树。并将该新树的根B放到原来的失衡点上。其中,A和C的子树不动。
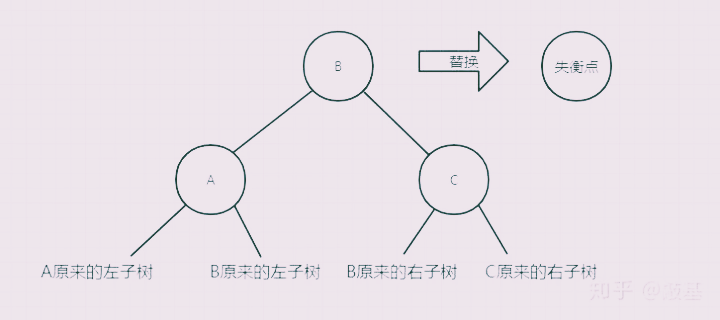
案例:
画出以序列{25,27,30,12,11,18,14,20,15,22}构造的一棵平衡二叉树
- 首先,按照左小右大的原则,画二叉树。依次插入25,27,30。
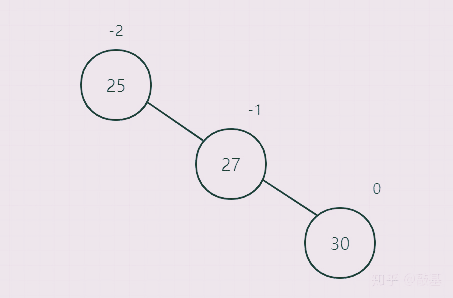
插入30后,二叉树失衡。
此时25为失衡点,从失衡点开始,经过两步寻找,找到27和30。则此时为RR旋转。将27代替失衡点,25作为左子树,30作为右子树重新构建平衡二叉树。
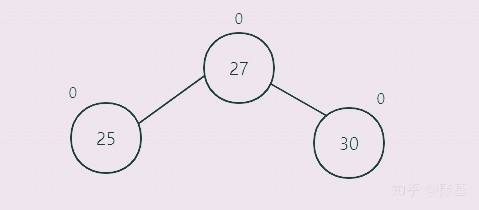
- 继续插入12,11。
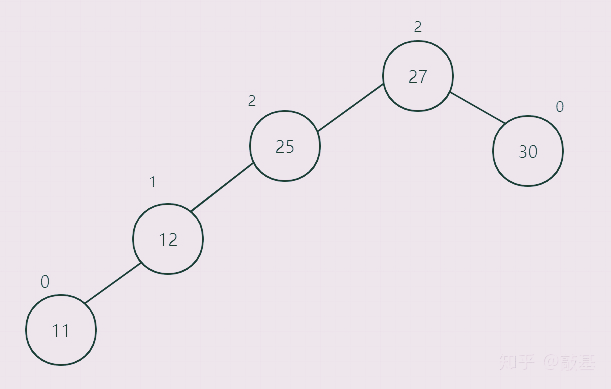
此时二叉树又失衡
失衡点为25,向下寻找,找到12和11,此时为LL旋转。将12代替失衡点,11作为左子树,25作为右子树,重新构建平衡二叉树。
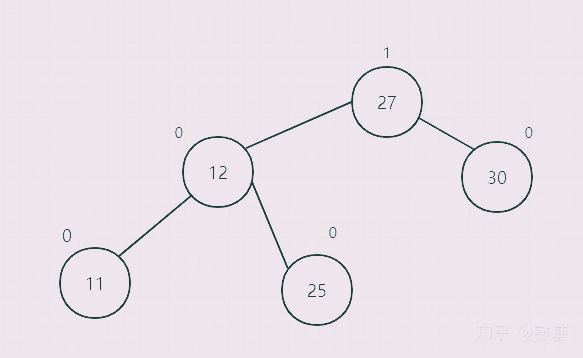
- 继续插入18。
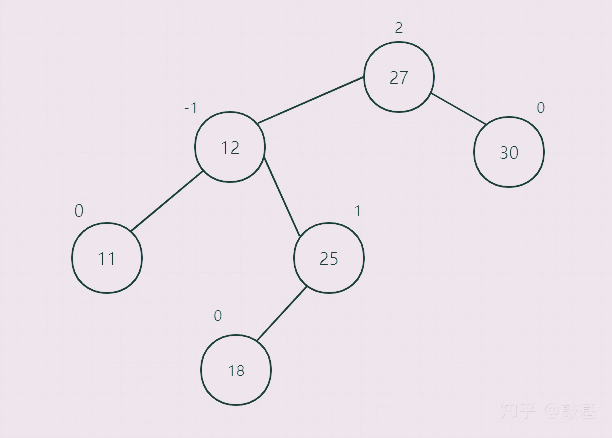
此时二叉树又失衡了
失衡点是27,从失衡点向下寻找,找到12和25,则为LR旋转。将25代替失衡点,左子树为12,其中左子树12的左子树为其本身的左子树,而右子树为25原先的左子树,即18。右子树为27,右子树27的右子树为其本身的右子树,而左子树为25原先的右子树,即null。
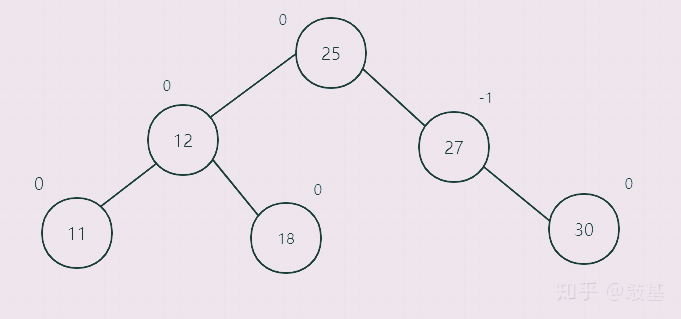
- 继续插入14,20,15。
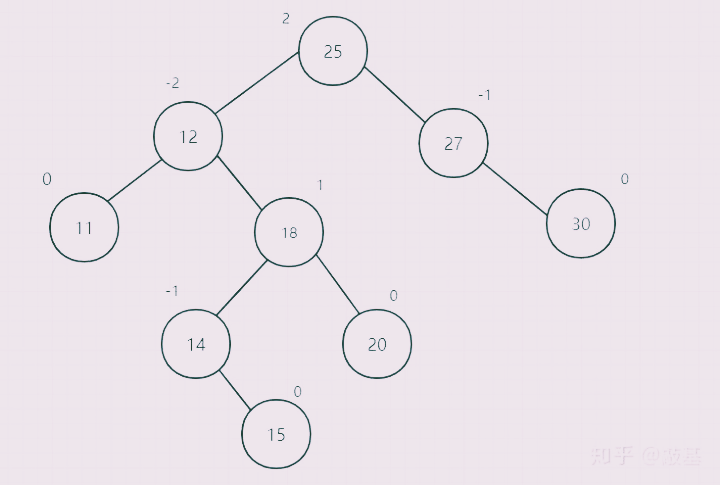
此时二叉树又失衡了,继续重复上述过程
插入点为15,失衡点为12。“寻找”路径记为“右左”,因此需要RL旋转。在12,18,14中,取“中位数”14作树根,12作左子树,18作右子树,生成新的平衡二叉树。且14的右子树根15“顺利成章”地放在18的左侧。
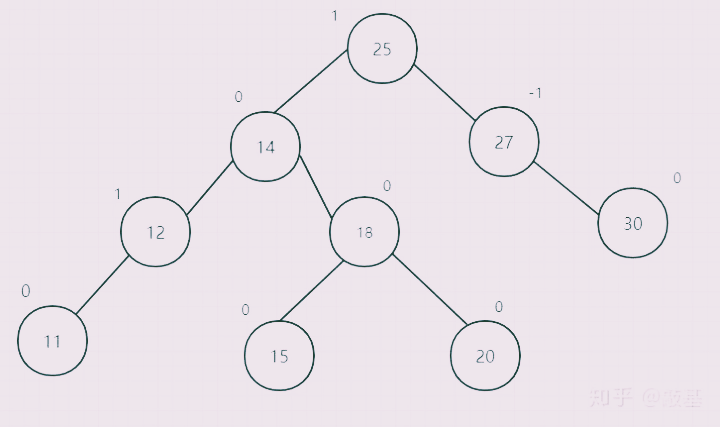
- 最后插入22。
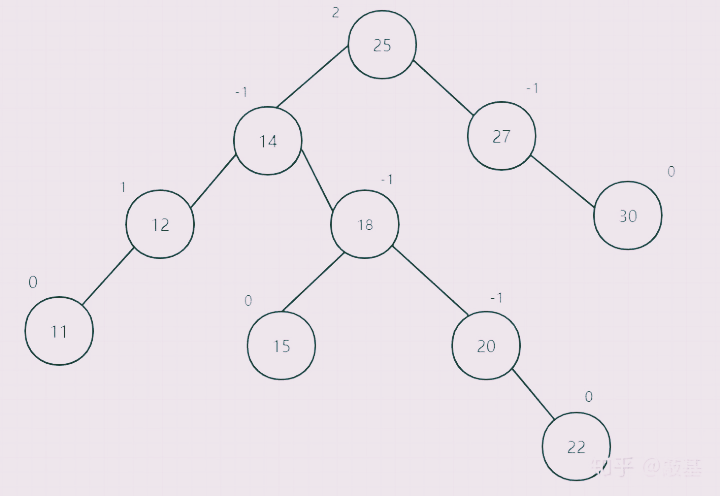
二叉树叕失衡了。
插入点为22,失衡点为25。“寻找”路径记为“左右”,因此需要LR旋转。在25,14,18中,取“中位数”18作树根,14作左子树,25作右子树,生成新的平衡二叉树。且18的左子树根15“顺理成章”地放在14的右侧,18的右子树根20“顺利成章”地放在25的左侧。(不懂请看旋转方法图解)并替换到失衡点25上。
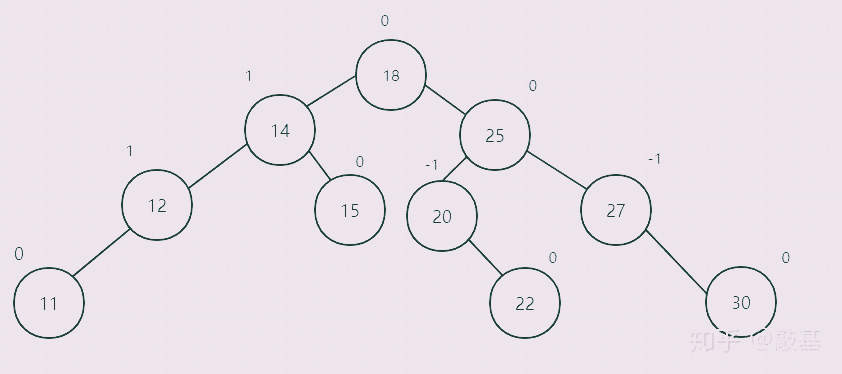
7.6红黑树
7.6.1红黑树的概念
红黑树是一种自平衡二叉查找树,它通过旋转和重新变色来保持平衡。它的每个节点都带有颜色属性,颜色为红色或黑色。
红黑树有一些特定的性质:
- 节点是红色或黑色。
- 根是黑色。
- 所有叶子都是黑色(叶子是NIL节点)。
- 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
这些约束确保了红黑树的关键特性:从根节点到叶子节点的最长的路径不大于最短路径的两倍。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树。
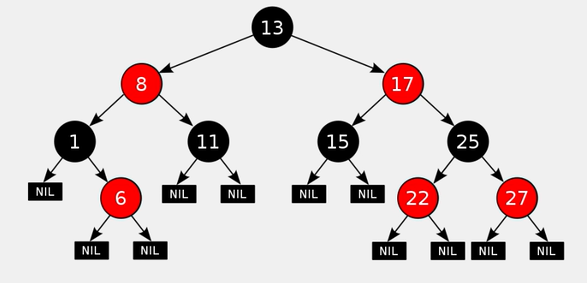
7.6.2红黑树和2-3-4树的联系
一棵2-3-4树可以转换为一棵红黑树,转换方法如下:
- 将2-3-4树中的每个2节点(即只包含一个关键字的节点)转换为一个黑色节点。
- 将2-3-4树中的每个3节点(即包含两个关键字的节点)转换为一个黑色节点和一个红色子节点。其中,红色子节点是黑色节点的左子节点或右子节点,取决于红色子节点中的关键字与黑色节点中的关键字的大小关系。
- 将2-3-4树中的每个4节点(即包含三个关键字的节点)转换为一个黑色节点和两个红色子节点。其中,两个红色子节点分别是黑色节点的左子节点和右子节点。
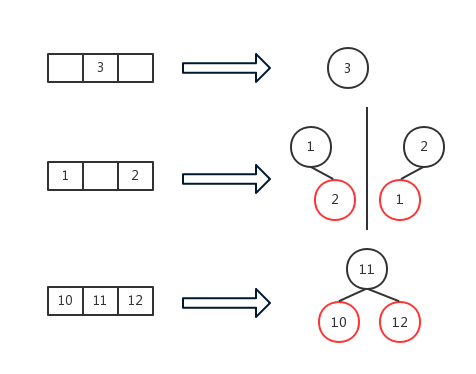
经过这样的转换后,我们就可以得到一棵与原来的2-3-4树等价的红黑树。这棵红黑树满足红黑树的所有性质,并且能够在插入和删除操作后通过旋转和重新着色来保持平衡。
同样地,一棵红黑树也可以转换为一棵2-3-4树。转换方法是将红黑树中的每个红色节点与其父节点合并,形成一个新的2-3-4树中的3节点或4节点。
如下是一个2-3-4树:
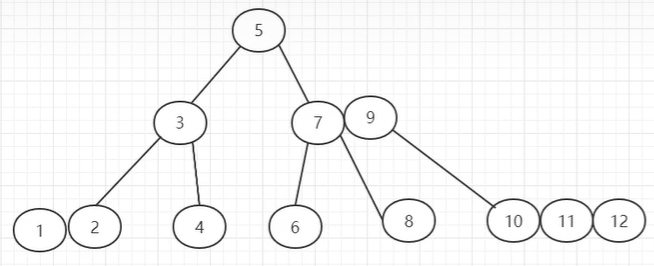
转换为对应的红黑树为:
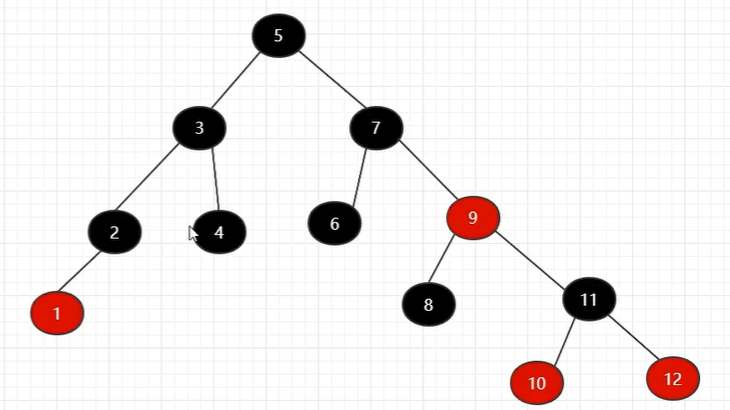
7.6.3红黑树的插入删除操作
7.6.3.1插入操作
在红黑树中插入一个新节点时,我们首先按照二叉查找树的方法将新节点插入到树中。新插入的节点被标记为红色。
然后,我们需要检查新插入的节点是否违反了红黑树的性质。如果新插入的节点是红色,并且它的父节点也是红色,那么就会违反红黑树的性质。此时,我们需要通过重新着色和旋转来调整树的结构,使其重新满足红黑树的性质。
重新着色和旋转的具体方法取决于新插入节点、它的父节点和祖父节点之间的关系。可能需要进行以下几种操作之一:
- 当前节点是根节点:把根节点改为黑色
- 当前节点的父节点是黑节点:保持不变
- 当前节点的父节点是红节点,并且当前节点的叔叔节点是红节点:把父节点和叔叔节点改为黑色,把祖父节点改为红色,把祖父节点作为当前节点,向上判断。
- 当前节点的父节点是红节点,并且父节点的兄弟节点不是红节点:四种情况
- 祖父节点->父节点->当前节点,是一直向右:做左旋操作,再把父节点改为黑色,之前的祖父节点改为红色
- 祖父节点->父节点->当前节点,是一直向左:做右旋操作,再把父节点改为黑色,之前的祖父节点改为红色
- 祖父节点->父节点->当前节点,是先向左再向右:先对当前节点做左旋操作,再对当前节点做右旋操作,然后把当前节点改为黑色,之前的祖父节点改为红色
- 祖父节点->父节点->当前节点,是先向右再向左:先对当前节点做右旋操作,再对当前节点做左旋操作,然后把当前节点改为黑色,之前的祖父节点改为红色
7.6.3.2删除操作
红黑树的删除操作包括查找到删除节点和删除节点以及删除之后的自平衡两部分。与红黑树插入操作类似,红黑树的删除操作也是通过重新着色(recoloring)和旋转(rotation)来保证每一次删除操作后依旧满足红黑树的属性的。在插入操作中,通过判断插入结点x的叔叔结点u的颜色来确定恰当的平衡操作。而删除操作中,是通过检查兄弟结点的颜色来决定恰当的平衡操作。
红黑树删除操作的复杂度在于删除节点的颜色,当删除的节点是红色时,直接拿其孩子节点补空位即可。
因为删除红色节点,性质5(从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点)仍能够被满足。但是当删除节点是黑色时,就需要进行一些额外的调整来保证红黑树的性质不被破坏。
具体来说,如果要删除一个黑色节点,我们需要考虑以下几种情况:
- 如果被删除节点有一个红色子节点,那么我们可以直接用这个红色子节点替换被删除节点,并将其重新着色为黑色。
- 如果被删除节点没有红色子节点,那么我们需要对其兄弟节点进行检查。如果兄弟节点是红色,那么我们可以通过旋转和重新着色来调整树的结构。
- 如果兄弟节点是黑色并且至少有一个红色子节点,那么我们可以通过旋转和重新着色来调整树的结构。
- 如果兄弟节点是黑色并且没有红色子节点,那么我们需要对其父亲节点进行递归调整。
7.6多路平衡搜索树
7.6.1二叉树存在的问题
二叉树的操作效率较高,但是也存在问题
- 在构建二叉树时,需要多次进行I/O操作(海量数据存在数据库或文件中),节点海量,构建二叉树时,速度有影响
- 节点海量,也会造成二叉树的高度很大,会降低操作速度
多叉树是一种树形结构,其中每个节点可以有多个子节点。在二叉树中,每个节点最多有两个子节点。如果允许每个节点可以有更多的数据项和更多的子节点,就是多叉树(multiway tree)。
多叉树通过重新组织节点,减少树的高度,能对二叉树进行优化。例如,2-3树和2-3-4树就是多叉树。
如下就是2-3树:
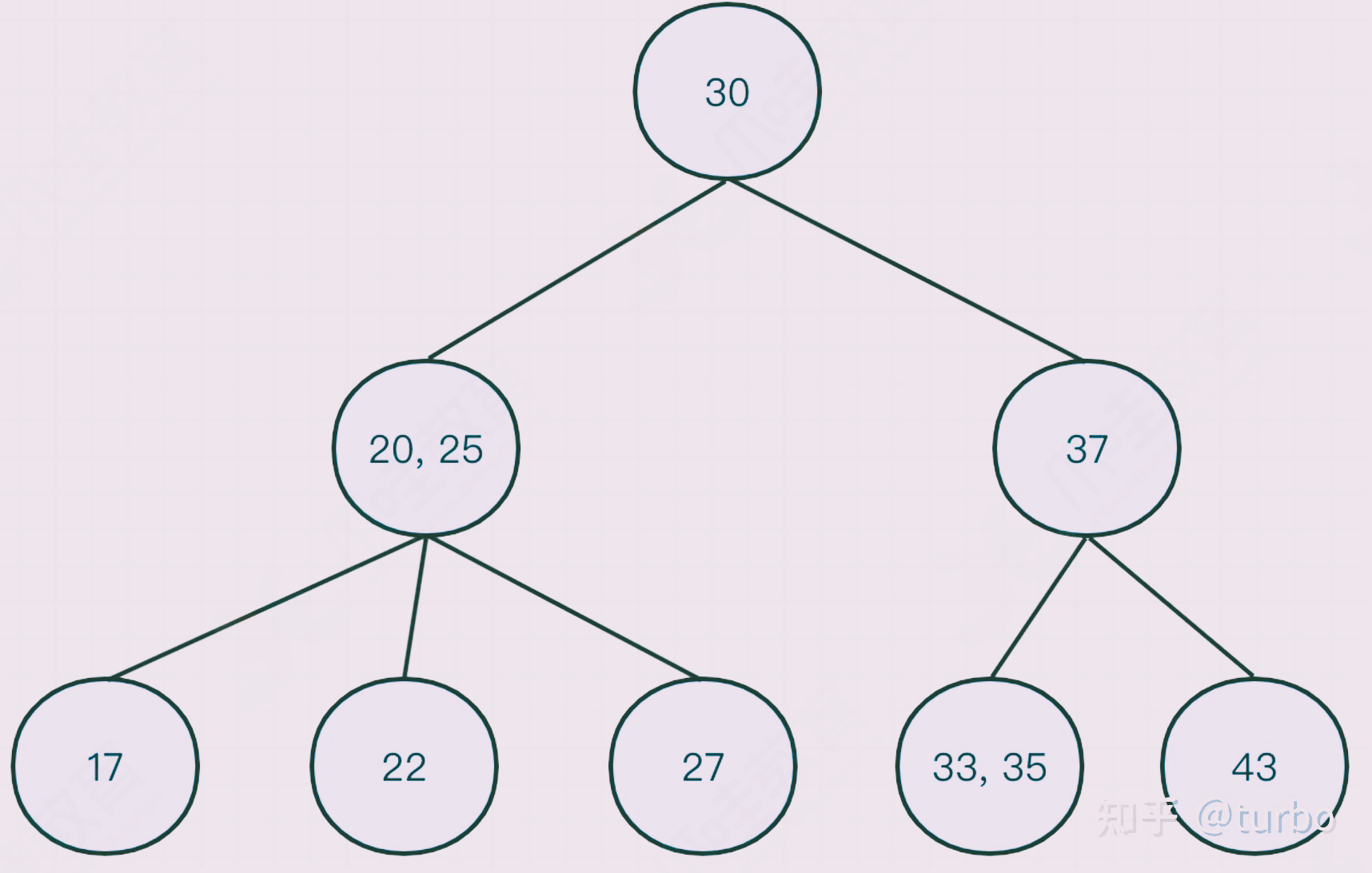
7.6.2概述
多路平衡搜索树是一种树形数据结构,它可以有多个子节点(这意味着每个节点可以有多于两个的分支)。与二叉搜索树不同,多路平衡搜索树的每个节点可以有多个关键字和多个子节点。这种数据结构通常用于磁盘访问和数据库索引,因为它能够减少磁盘访问次数。
常见的多路平衡搜索树包括B树、B+树、2-3树、2-3-4树等。B树是一种自平衡的m阶树,它具有一些特定的性质,例如每个非叶子节点至少有两个子节点,所有叶子节点都在同一层等。B+树是B树的变体,它的非叶子节点只存储索引,而不存储实际数据,所有数据都存储在叶子节点中。2-3树和2-3-4树都是B树的特例,其中2-3树是3阶B树,2-3-4树是4阶B树。
这些数据结构都有各自的优缺点和适用场景。例如,B+树通常用于数据库索引和文件系统,因为它能够减少磁盘访问次数。这些数据结构通过旋转和分裂来保持平衡,并且能够在最坏情况下保证高效的查找、插入和删除操作。
7.6.3 2-3树
2-3树是最简单的B树结构,具有如下特点:
- 2-3树的所有叶子节点都在同一层(只要是B树都满足这个条件)
- 有两个子节点的节点叫二节点,二节点要么没有子节点,要么有两个子节点.
- 有三个子节点的节点叫三节点,三节点要么没有子节点,要么有三个子节点.
- 2-3树 是由二节点和三节点构成的树。
将数列{16, 24, 12, 32, 14, 26,34, 10, 8, 28, 38, 20}构建成2-3树,并确保数据插入的大小顺序。
插入规则:
插入规则:
- 2-3树的所有叶子节点都在同一层(只要是B树都满足这个条件)
- 有两个子节点的节点叫二节点,二节点要么没有子节点,要么有两个子节点
- 有三个子节点的节点叫三节点,三节点要么没有子节点,要么有三个子节点
- 当按照规则插入一个数到某个节点时, 不能满足上面三个要求,就需要拆,先向上拆,如果上层满,则拆本层,拆后仍然需要满足上面3个条件。
- 对于三节点的子树的值大小仍然遵守
- 添加16
[16]- 添加24,大于16,与16构成一个
三节点。(因为不满足二节点)
[16,24]- 添加12,小于16,不能放到
[16,24]当中,因为会构成一个四节点。所以拆分三节点。
16
/ \
12 24 - 添加32,大于24,所以和24组成
三节点
16
/ \
12 [24,32]- 添加14,14大于12,所以可以和12组成
三节点
16
/ \
[12,14] [24,32]- 添加26,24大于26,但是不能放在
[24,32]中,因为会组成四节点,所以这个时候就往上拆
[16,26]
/ | \
[12,14] 24 32- 添加34,大于32,和32组成
二节点
[16,26]
/ | \
[12,14] 24 [32,34]- 添加10,应当在10- 12-14这个位置,但是这时满了,因此向上层看,16-26也满了,因此将10-12-14拆成10 <-12->14,因为其它拆法,不能满足二节点或三节点的要求。但是这时,叶子节点没有全部在同一层,需要调整26这个值到下面。
16
/ \
12 26
/ \ / \
10 14 24 [32,34]- 添加28,28大于26,但是不能够直接添加到26后面组成
三节点,因为拆分后 32 > 28。所以将32上移,28为三节点的中间节点。
16
/ \
12 [26,32]
/ \ / | \
10 14 24 28 34- 添加38,直接和38组成
四节点。
16
/ \
12 [26,32]
/ \ / | \
10 14 24 28 [34,28]- 添加20,大于16,小于26,小于24,所以和24直接组成
三节点
16
/ \
12 [26,32]
/ \ / | \
10 14 [20,24] 28 [34,28]自此2-3树构建完成。
7.6.4 2-3-4树
2-3-4 树其实就是 2-3 树的概念扩展,它多了一个 4 结点。
2-3-4树是四阶的B树(Balance Tree),他属于多路查找树,它的结构有以下限制:
所有叶子节点都拥有相同的深度。
节点只能是2-节点3-节点4节点之一。
- 2-节点:包含1个元素的节点,有2个子节点;
- 3-节点:包含2个元素的节点有3个仔节点;
- 4-节点:包含3个元素的节点,有4个子节点
所有节点必须至少包含1个元素
元素始终保持排序顺序,整体上保持二叉查找树的性质,即父结点大于左子结点,小于右子结点;
而且结点有多个元素时,每个元素必须大于它左边的和它的左子树中元素。
下面是一个典型的2-3-4树
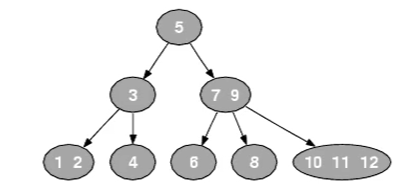
2-3-4树的查询操作像普通的二叉搜索树,非常简单,但由于其结点元素数不确定,在一些编程语言中实现起来并不方便, 实现
一般使用它的等同一红黑树。
7.6.4B树
B 树是一种平衡的多路查找树,2-3 树和 2-3-4 树都是 B 树的特例,结点所拥有的最大孩子树称为 B 树的阶,因此,2-3 树是 3 阶 B 树,2-3-4 树是 4 阶 B 树。
m为B树的阶数,那么该树就有以下特性:
- 每个节点最多m-1个关键字,也就是说每个节点最多有m个分叉
- 所有叶子结点都处于同一层次
- 和平衡二叉树类似,关键字的左侧数据都比关键字小,关键字的右侧数据都比关键字大
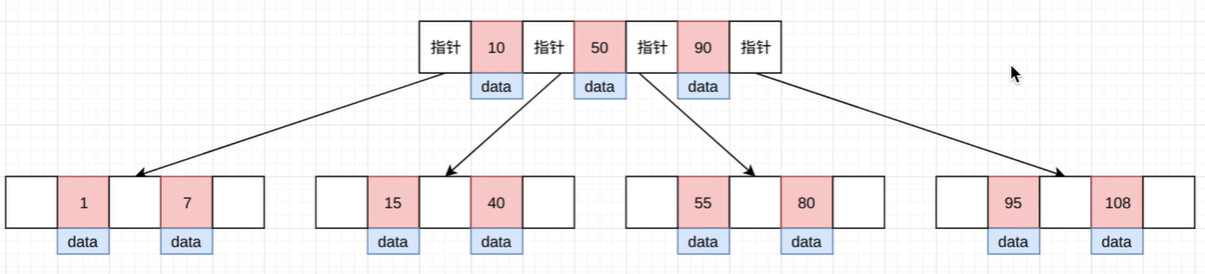
7.6.5B+树
B+ 树与 B 树的差异在于:
- B树的每个节点既包含关键字,也包含数据。而B+树的非叶子节点仅包含关键字,数据仅存储在叶子节点中。
- B+树的叶子节点之间通过指针相连,形成一个单向链表结构,便于范围查找。而B树的叶子节点之间没有直接联系。
- 在一棵m阶的B+树中,每个非叶子节点最多可以存储m-1个关键字,每个叶子节点最多可以存储m个数据。而在一棵m阶的B树中,每个节点最多可以存储m-1个关键字。